
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,4),与直线y=﹣x+1相交于A、B两点,其中点A在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).点M是直线AB上方的抛物线上一动点,过M作MP丄x轴,垂足为点P,交直线AB于点N,设点M的横坐标为m.
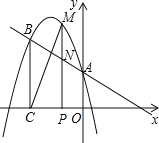
(1)求抛物线的解析式;
(2)当m为何值时,线段MN取最大值?并求出这个最大值.
【答案】(1)y=﹣x2﹣4x+1;(2)当m=﹣![]() 时,MN有最大值是
时,MN有最大值是![]() .
.
【解析】
试题分析:(1)首先求得A和B的坐标,然后利用待定系数法求得抛物线的解析式;
(2)当x=m是,M和N的纵坐标即可利用m表示出来,然后根据二次函数的性质求得MN的最大值.
解:(1)在y=﹣x+1中,令x=0,解得y=1,则A的坐标是(0,1).
在y=﹣x+1中,令x=﹣3,则y=3+1=4,则B的坐标是(﹣3,4).
根据题意得: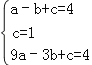 ,
,
解得: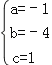 .
.
则抛物线的解析式是y=﹣x2﹣4x+1;
(2)当x=m是,M的纵坐标是﹣m2﹣4m+1,N的纵坐标是﹣m+1,
则MN=(﹣m2﹣4m+1)﹣(﹣m+1)=﹣m2﹣3m=﹣(m2+3m)=﹣(m+![]() )2+
)2+![]() .
.
则当m=﹣![]() 时,MN有最大值是
时,MN有最大值是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列命题中正确的有( )个
①三个内角对应相等的两个三角形全等;
②三条边对应相等的两个三角形全等;
③有两角和一边分别对应相等的两个三角形全等;
④等底等高的两个三角形全等.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
①﹣10+8
②﹣20+(﹣14)﹣(﹣18)﹣13
③2﹣2÷(﹣![]() )×3
)×3
④﹣14﹣![]() ×[3﹣(﹣3)2]
×[3﹣(﹣3)2]
⑤﹣24×(﹣![]() +
+![]() ﹣
﹣![]() )
)
⑥﹣22+3×(﹣2)﹣(﹣4)2÷(﹣8)﹣(﹣1)100.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
![]()
(1)线段AB的长度为 个单位长度,点M表示的数为 .
(2)当点Q运动到点M时,点P运动到点N,则MN的长度为 个单位长度.
(3)设点P运动的时间为t秒.是否存在这样的t,使PA+QA为5个单位长度?如果存在,请求出t的值和此时点P表示的数;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
甲、乙两人同时从相距25千米的A地去B地,甲骑车乙步行,甲的速度是乙的速度的3倍,甲到达B地停留40分钟,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好3小时,求两人的速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=∠2,∠C=∠D,AC、BD交于E点,下列结论中不正确的是( )
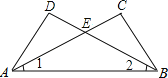
A.∠DAE=∠CBE
B.△DEA不全等于△CEB
C.CE=DE
D.△EAB是等腰三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com