练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．如图，点A表示的实数是（　　）
    A．$\sqrt{3}$B．$\sqrt{5}$C．$-\sqrt{5}$D．$-\sqrt{3}$

    分析 根据勾股定理可求得OA的长为$\sqrt{5}$，再根据点A在原点的左侧，从而得出点A所表示的数．

    解答 解：如图，OB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$，

    ∵OA=OB，
    ∴OA=$\sqrt{5}$，
    ∴点A在数轴上表示的实数是-$\sqrt{5}$，
    故选：C．

    点评 本题考查了实数和数轴，以及勾股定理，原点左边的数是负数．解决本题的关键是利用勾股定理求出OB的长．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．分解因式：a3-4a．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．计算：$\frac{2a}{{{a^2}-16}}-\frac{1}{a-4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．下面哪个点在函数y=$\frac{1}{2}$x+1的图象上（　　）
    A．（-2，0）B．（-2，1）C．（2，0）D．（2，1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

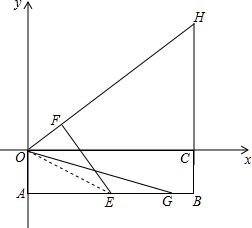    4．如图，矩形OABC中，OA在y轴的负半轴上，OC在x轴的正半轴上，OA=1，OC=4，E是AB的中点，将矩形沿OE折叠，点A与点F重合，延长OF、BC交于点H，G是射线AB上一点，将△OAG绕点O旋转，使得点A落在OE上，记旋转后的三角形为△OA′G′，A′G′与OH交于点M，若∠MHG′=∠MHB，则AG的长为$\frac{2+20\sqrt{5}}{11}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．将下列各多项式因式分解
    （1）15a2+5a
    （2）x5-x3
    （3）a3b-4a2b2+4ab3
    （4）1-x2-y2+x2y2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．已知一个直角三角形的两条直角边的差为2，两条直角边的平方和为8，则这个直角三角形的面积是1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

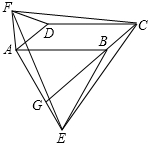    18．如图，在?ABCD中，分别以AB、AD为边向外作等边△ABE，△ADF，延长CB交AE于点G，点G落在点A、E之间，连接EF、CF．则以下四个结论：
    ①CG⊥AE；
    ②△CDF≌△EBC；
    ③∠CDF=∠EAF；
    ④△ECF是等边三角形．
    其中一定正确的是②③④．（把正确结论的序号都填上）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．在Rt△ABC中，∠ACB=90°，经过点B的直线l（l不与直线AB重合）与直线BC的夹角等于∠ABC，分别过点C、点A作直线l的垂线，垂足分别为点D、点E．
    （1）如图1，当点E与点B重合时，若AE=4，判断以C点为圆心CD长为半径的圆C与直线AB的位置关系并说明理由；
    （2）如图2，当点E在DB延长线上时，求证：AE=2CD；
    （3）记直线CE与直线AB相交于点F，若$\frac{CF}{EF}=\frac{5}{6}$，CD=4，求BD的长．

    查看答案和解析>>

    同步练习册答案