
如图,在平面直角坐标系中,二次函数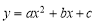 (
(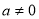 )的图象经过点A(-1,0)、点B(3,0)、点C(0,3).
)的图象经过点A(-1,0)、点B(3,0)、点C(0,3).

(1)求此抛物线的解析式及顶点D的坐标;
(2)连结AC、CD、BD,试比较∠BCA与∠BDC的大小,并说明理由;
(3)若在x轴上有一动点M,在抛物线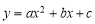 上有一动点N,则M、N、B、C四点是否能构成平行四边形,若存在,请求出所有适合的点M的坐标;若不存在,请说明理由.
上有一动点N,则M、N、B、C四点是否能构成平行四边形,若存在,请求出所有适合的点M的坐标;若不存在,请说明理由.
(1)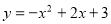 ,D的坐标为(1,4).(2)∠BCA∠B DC,理由见解析,(3)(1,0)、(5,0)、(
,D的坐标为(1,4).(2)∠BCA∠B DC,理由见解析,(3)(1,0)、(5,0)、(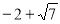 ,0)、(
,0)、(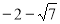 ,0).
,0).
【解析】
试题分析:(1)分别把点A(-1,0)、点B(3,0)、点C(0,3)代入 ,求出a、b、c的值即可,再进行配方求出点D的坐标.
,求出a、b、c的值即可,再进行配方求出点D的坐标.
(2)分别求出CD,BD,CB,AC的长度,即可得出△CDB∽△OAC,故∠BCA=∠BDC
(3)设点M的坐标为(t,0)则N的坐标分别是(3-t,3),(t-3,3),(t+3,-3)代入解析式t的值.
试题解析:(1)∵点A、B、C在抛物线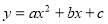 上,
上,
∴ 解得
解得
∴此抛物线为: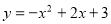
由
∴抛物线的顶点D的坐标为(1,4).
(2)连结BC,

由点C(0,3)、B(3,0)、D(1,4)
可得CD=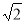 ,BD=
,BD=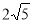 ,CB=
,CB=
由点C(0,3)、A(-1,0),可得AC=
由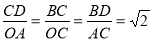
∴ △CDB∽△OAC
∴∠BCA=∠BDC
(3)设点M的坐标为(t,0)
则由C(0,3)、B(3,0)、M(t,0)可以得到
若能构成平行四边形时点N的坐标有三种可能,
分别是(3-t,3),(t-3,3),(t+3,-3)
∵点N在抛物线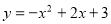 上
上
当把(3-t,3)代入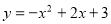 时,
时,
可得t=1或t=3(点M与点B重合,舍去);
当把(t-3,3)代入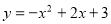 时,
时,
可得t=5或t=3(点M与点B重合,舍去);
当把(t+3,-3)代入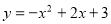 时,
时,
可得t=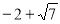 或t=
或t=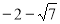 ,
,
综上可知,M的坐标为(1,0)、(5,0)、(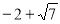 ,0)、(
,0)、(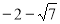 ,0).
,0).
考点:二次函数综合题
考点分析: 考点1:二次函数 定义: (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。  (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:  (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);  (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0)  与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。  (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性


科目:初中数学 来源:2014-2015学年山西省大同市矿区七年级上学期期末质量检测数学试卷(解析版) 题型:填空题
把正方体的6个面分别涂上不同的颜色,并画上朵数不等的花,各面上的颜色与花朵数的情况列表如下:
颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
花朵数 | 6 | 5 | 4 | 3 | 2 | 1 |
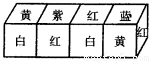
现将上述大小相同,颜色、花朵分布完全一样的四个正方体拼成一个在同一平面上放置的长方体,如下图所示,那么长方体的下底面共有______朵花.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于两个不同的点A、B,其中点A在x轴上.
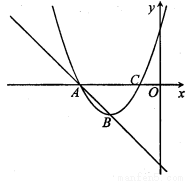
(1)则A点坐标为 ;
(2)若点B为该抛物线的顶点,求m、n的值;
(3)在(2)条件下,设该抛物线与x轴的另一个交点为C,请你探索在平面内是否存在点D,使得△DAC与△DCO相似?如果存在,求出点D的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级上学期期末考试数学试卷(解析版) 题型:选择题
在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,下列等式一定能成立的有
A.sinA=sinB B.a=c·sinB C.sin2A+cos2B=1 D.sinA=tanA·cosA
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省南通市崇川区九年级3月月考数学试卷(解析版) 题型:解答题
如图,在Rt△ABC中,∠ACB90°,AC3,AB5.
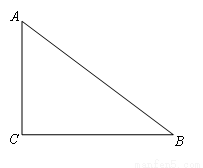
(1)用“直尺和圆规”在BC边上找一点O,使以点O为圆心,OC为半径的圆与AB相切,并画出⊙O(保留作图痕迹,不写作法);
(2)求(1)中所画圆的半径.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市九年级下学期第一次质量检测数学试卷(解析版) 题型:解答题
问题情境:如图1,P是⊙O外的一点,直线PO分别交⊙O于点A、B,则PA是点P到⊙O上的点的最短距离.
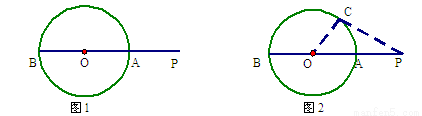
探究:
请您结合图2给予证明,
归纳:
圆外一点到圆上各点的最短距离是:这点到连接这点与圆心连线与圆交点之间的距离.
图中有圆,直接运用:
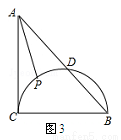
如图3,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是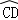 上的一个动点,连接AP,则AP的最小值是 .
上的一个动点,连接AP,则AP的最小值是 .
图中无圆,构造运用:
如图4,在边长为2的菱形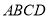 中,∠
中,∠ =60°,
=60°,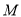 是
是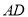 边的中点,
边的中点,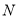 是
是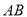 边上一动点,将△
边上一动点,将△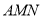 沿
沿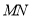 所在的直线翻折得到△
所在的直线翻折得到△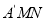 ,连接
,连接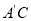 ,请求出
,请求出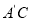 长度的最小
长度的最小
值.

【解析】
由折叠知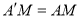 ,又M是AD的中点,可得
,又M是AD的中点,可得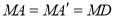 ,故点
,故点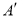 在以AD为直径的圆上.如图8,以点M为圆心,MA为半径画⊙M,过M作MH⊥CD,垂足为H,(请继续完成下列解题过程)
在以AD为直径的圆上.如图8,以点M为圆心,MA为半径画⊙M,过M作MH⊥CD,垂足为H,(请继续完成下列解题过程)
迁移拓展,深化运用:
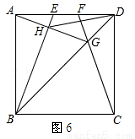
如图6,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省丹阳市十乡九年级下学期第一次联考数学试卷(解析版) 题型:选择题
若实数x、y满足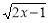 +2
+2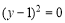 ,则
,则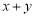 的值等于 ( )
的值等于 ( )
A.1 B.  C. 2 D.
C. 2 D.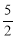
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com