
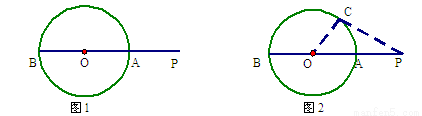
问题情境:如图1,P是⊙O外的一点,直线PO分别交⊙O于点A、B,则PA是点P到⊙O上的点的最短距离.
探究:
请您结合图2给予证明,
归纳:
圆外一点到圆上各点的最短距离是:这点到连接这点与圆心连线与圆交点之间的距离.
图中有圆,直接运用:
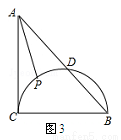
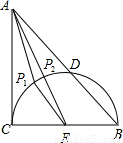
如图3,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是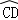 上的一个动点,连接AP,则AP的最小值是 .
上的一个动点,连接AP,则AP的最小值是 .
图中无圆,构造运用:
如图4,在边长为2的菱形 中,∠
中,∠ =60°,
=60°,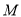 是
是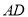 边的中点,
边的中点,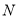 是
是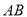 边上一动点,将△
边上一动点,将△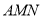 沿
沿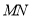 所在的直线翻折得到△
所在的直线翻折得到△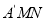 ,连接
,连接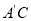 ,请求出
,请求出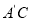 长度的最小
长度的最小
值.

【解析】
由折叠知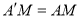 ,又M是AD的中点,可得
,又M是AD的中点,可得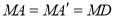 ,故点
,故点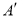 在以AD为直径的圆上.如图8,以点M为圆心,MA为半径画⊙M,过M作MH⊥CD,垂足为H,(请继续完成下列解题过程)
在以AD为直径的圆上.如图8,以点M为圆心,MA为半径画⊙M,过M作MH⊥CD,垂足为H,(请继续完成下列解题过程)
迁移拓展,深化运用:
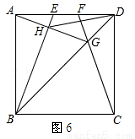
如图6,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 .
探究:证明见解析;图中有圆,直接运用: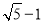 ;图中无圆,构造运用:
;图中无圆,构造运用: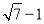 ;迁移拓展,深化运用:
;迁移拓展,深化运用: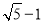 .
.
【解析】
试题分析:探究:在⊙O上任取一点C(不为点A、B),连接PC、OC.由PO<PC+OC,PO=PA+OA,OA=OC,得:PA<PC即可得出结论;
图中有圆,直接运用:找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,可见,AP1+EP1>AE,即AP2是AP的最小值,再根据勾股定理求出AE的长,然后减掉半径即可.
图中无圆,构造运用:
根据题意得出A′的位置,进而利用锐角三角函数关系求出A′C的长即可.
迁移拓展,深化运用:
点H是在Rt△AHB,AB直径的半圆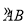 上运动当O、H、D三点共线时,DH长度最小
上运动当O、H、D三点共线时,DH长度最小
试题解析:探究:
如图2,在⊙O上任取一点C(不为点A、B),连接PC、OC.
∵PO<PC+OC,PO=PA+OA,OA=OC,
∴PA<PC,
∴PA是点P到⊙O上的点的最短距离.
图中有圆,直接运用:
找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,
可见,AP1+EP1>AE,
即AP2是AP的最小值,
∵AE= ,P2E=1,
,P2E=1,
∴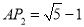
图中无圆,构造运用:
由模型可知,当点 在CM上时,
在CM上时,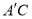 长度取得最小值.
长度取得最小值.
在Rt△MDH中 ,
,
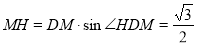 .
.
在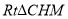 中,
中,
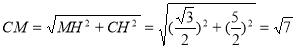 ,
,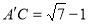
迁移拓展,深化运用:
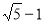
考点:圆的综合题.
考点分析: 考点1:圆 圆,圆的有关性质与圆的有关计算是近几年各地中考命题的重点内容。题型以填空题,选择题和解答题为主,也有以阅读理解,条件开放,结论开放探索题作为新的题型,分值一般是6-12分,难易度为中,考察内容:①圆的有关性质的应用。垂径定理是重点。② 直线和圆,圆和圆的位置关系的判定及应用。③弧长,扇形面积,圆柱,圆锥的侧面积和全面积的计算④圆与相似三角形,三角函数的综合运用以及有关的开放题,探索题。突破方法:①熟练掌握圆的有关行政,掌握求线段,角的方法,理解概念之间的相互联系和知识之间的相互转化。②理解直线和原的三种位置关系,掌握切线的性质和判定的歌,会根据条件解决圆中的动态问题。③掌握有两圆半径的和或差与圆心距的大小关系来盘底的那个两个圆的位置关系,对中考试题中常出现的阅读理解题,探索题,要灵活运用圆的有关性质,进行合理推理与计算。④掌握弧长,扇形面积计算公式。⑤理解圆柱,圆锥的侧面展开图⑥对组合图形 的计算要灵活运用计算方法解题。 试题属性

科目:初中数学 来源:2014-2015学年山西农业大学附属中学七年级上学期期末考试数学试卷(解析版) 题型:选择题
一件标价为300元的棉袄,按七折销售仍可获利20元。设这件棉袄的成本价为x元,根据题意,下面所列方程正确的是( )
A、300×7-x=20 B、300×0.7-x=20
C、300×0.7=x-20 D、300×7=x-20
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省南通市崇川区九年级3月月考数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,二次函数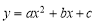 (
(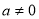 )的图象经过点A(-1,0)、点B(3,0)、点C(0,3).
)的图象经过点A(-1,0)、点B(3,0)、点C(0,3).

(1)求此抛物线的解析式及顶点D的坐标;
(2)连结AC、CD、BD,试比较∠BCA与∠BDC的大小,并说明理由;
(3)若在x轴上有一动点M,在抛物线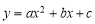 上有一动点N,则M、N、B、C四点是否能构成平行四边形,若存在,请求出所有适合的点M的坐标;若不存在,请说明理由.
上有一动点N,则M、N、B、C四点是否能构成平行四边形,若存在,请求出所有适合的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省南通市崇川区九年级3月月考数学试卷(解析版) 题型:选择题
如图是正方体的展开图,则原正方体相对两个面上的数字之和的最大值是( )
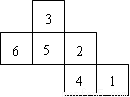
A.6 B.7 C.8 D.9
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市九年级下学期第一次质量检测数学试卷(解析版) 题型:解答题
近期,中国足球改革方案由中央深改小组审议通过,中国足球迎来春天的气息.甲、乙、丙三人进行踢足球训练.球从一个人脚下随机传到另外一个人脚下,共传球三次.
(1)若开始时球在甲脚下,求经过三次传球后,球传回甲脚下的概率是多少?
(2)若乙想使球经过三次传递后,球落在自己脚下的概率最大,乙会让球开始时在谁脚下?请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省丹阳市十乡九年级下学期第一次联考数学试卷(解析版) 题型:解答题
(本小题满分8分)某技工培训中心有钳工20名、车工30名. 现将这50名技工中的15人派往A地工作,35人派往B地工作,两地技工的工资情况如下表:
工种 属地 | 钳工 | 车工 |
| 1800(元/月) | 1600(元/月) |
| 1600(元/月) | 1200(元/月) |
设派往A地x名钳工时,这50名技工的月工资总额为y元.
(1)派往B地___________名钳工,派往B地___________名车工;
(2)求y关于x的函数关系式;
(3)若A地钳工的月工资总额不小于B地钳工的月工资总额,派往A地多少名钳工,可使这50名技工的月工资总额最高?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com