
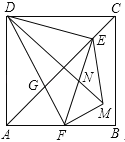
【题目】如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB的中点,则△EMN的周长是 .
【答案】
【解析】
试题解析:如图1,过E作PQ⊥DC,交DC于P,交AB于Q,连接BE,
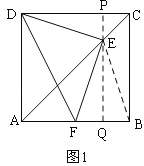
∵DC∥AB,
∴PQ⊥AB,
∵四边形ABCD是正方形,
∴∠ACD=45°,
∴△PEC是等腰直角三角形,
∴PE=PC,
设PC=x,则PE=x,PD=4﹣x,EQ=4﹣x,
∴PD=EQ,
∵∠DPE=∠EQF=90°,∠PED=∠EFQ,
∴△DPE≌△EQF,
∴DE=EF,
易证明△DEC≌△BEC,
∴DE=BE,
∴EF=BE,
∵EQ⊥FB,
∴FQ=BQ=![]() BF,
BF,
∵AB=4,F是AB的中点,
∴BF=2,
∴FQ=BQ=PE=1,
∴CE=![]() ,
,
Rt△DAF中,DF=![]() ,
,
∵DE=EF,DE⊥EF,
∴△DEF是等腰直角三角形,
∴DE=EF=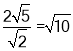 ,
,
∴PD=![]() =3,
=3,
如图2,
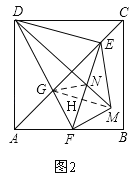
∵DC∥AB,
∴△DGC∽△FGA,
∴![]() ,
,
∴CG=2AG,DG=2FG,
∴FG=![]() ,
,
∵AC=![]() ,
,
∴CG=![]() ,
,
∴EG=![]() ,
,
连接GM、GN,交EF于H,
∵∠GFE=45°,
∴△GHF是等腰直角三角形,
∴GH=FH=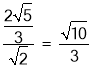 ,
,
∴EH=EF﹣FH=![]() ,
,
∴∠NDE=∠AEF,
∴tan∠NDE=tan∠AEF=![]() ,
,
∴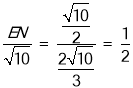 ,
,
∴EN=![]() ,
,
∴NH=EH﹣EN=![]() ,
,
Rt△GNH中,GN=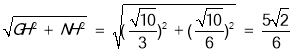 ,
,
由折叠得:MN=GN,EM=EG,
∴△EMN的周长=EN+MN+EM=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠A=90°,DE∥BC,F,G,H,I分别是DE,BE,BC,CD的中点,连接FG,GH,HI,IF,FH,GI.对于下列结论:①∠GFI=90°;②GH=GI;③GI= ![]() (BC﹣DE);④四边形FGHI是正方形.其中正确的是(请写出所有正确结论的序号).
(BC﹣DE);④四边形FGHI是正方形.其中正确的是(请写出所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个寻宝游戏的寻宝通道由正方形ABCD的边组成,如图1所示.为记录寻宝者的行进路线,在AB的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图象大致如图2所示,则寻宝者的行进路线可能为( )
A.A→B
B.B→C
C.C→D
D.D→A
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 是
是![]() 的中线,
的中线,![]() 是线段
是线段![]() 上一点(不与点
上一点(不与点![]() 重合),
重合),![]() 交
交![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() .
.
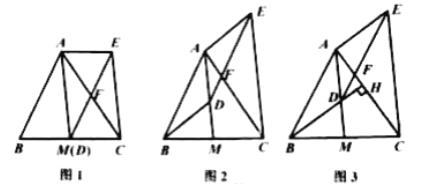
(1)如图1,当点![]() 与
与![]() 重合时,求证:四边形
重合时,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,当点![]() 不与
不与![]() 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,且
,且![]() .当
.当![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k=![]() ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1 , A2 , A3 , …在射线ON上,点B1 , B2 , B3 , …在射线OM上,△A1B1A2 , △A2B2A3 , △A3B3A4 , …均为等边三角形,若OA1=2,则△A5B5A6的边长为 . 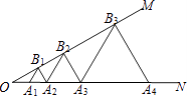
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com