
【题目】如图,抛物线y=﹣x2﹣2x+3的图象与x轴交于A.B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A,B,C,D的坐标;
(2)判断以点A,C,D为顶点的三角形的形状,并说明理由;
(3)点M( m,0)(﹣3<m<﹣1)为线段AB上一点,过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,得矩形PQNM,当矩形PQMN的周长最大时,m的值是多少?并直接写出此时△AEM的面积.
【答案】
(1)
解:由抛物线y+﹣x2﹣2x+3可得,当x=0时,y=0,即C(0,3).
当y=0,﹣x2﹣2x+3=0,解得,x=﹣3或x=l,令x=0,得y=3,
∴A(﹣3,0),B(1,0),C(0,3),
把y=﹣x2﹣2x+3化为顶点式为y=﹣(x+1)2+4,
∴D(﹣1,4)
(2)
解:结论:△ACD是直角三角形,理由如下,
连接CD、AD,设抛物线的对称轴交AC于点H,过点C作CF⊥DH于点F,则F(﹣1,3).
由A(﹣3,0),C(0,3)得直线AC的解析式为y=x+3,
把x=﹣1代入y=x+3得,y=2,即H(﹣1,2),
∴DF=4﹣3=1,FH=3﹣2=1,
∴DF=FH=CF=1,
∴∠HCD=90°,
∴△ACD是直角三角形
(3)
解:由D(﹣1,4)可知,对称轴为x=﹣1,
∵M(m,0),∴PM=﹣m2﹣2m+3,MN=(﹣m﹣1)×2=﹣2m﹣2,
∴矩形PMNQ的周长=2(PM+MN)
=(﹣m2﹣2m+3﹣2m﹣2)×2
=﹣2m2﹣8m+2,
∵﹣2m2﹣8m+2=﹣2(m+2)2+10,
∴m=﹣2时,矩形的周长最大,
∵A(﹣3,0),C(0,3),设直线AC解析式为y=kx+b,
则 ![]() 解得:
解得: ![]() ,
,
∴解析式y=x+3,当x=﹣2时,则E(﹣2,1),
∴EM=1,AM=1,
∴S= ![]() AMEM=
AMEM= ![]() .
.

【解析】(1)通过解析式即可得出C点坐标,令y=0,解方程得出方程的解,即可求得A、B的坐标.(2)结论:△ACD是直角三角形.连接CD、AD,设抛物线的对称轴交AC于点H,过点C作CF⊥DH于点F,只要证明DF=FH=CF即可解决问题.(3)设M点横坐标为m,则PM=﹣m2﹣2m+3,MN=(﹣m﹣1)×2=﹣2m﹣2,矩形PMNQ的周长d=﹣2m2﹣8m+2,将﹣2m2﹣8m+2配方,根据二次函数的性质,即可得出m的值,然后求得直线AC的解析式,把x=m代入可以求得三角形的边长,从而求得三角形的面积.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() 与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )
与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( ) 
A.(4,3)
B.(5, ![]() )
)
C.(4, ![]() )
)
D.(5,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣ ![]() x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
(1)求抛物线的解析式及它的对称轴方程;
(2)求点C的坐标,连接AC、BC并求线段BC所在直线的解析式;
(3)试判断△AOC与△COB是否相似?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出∠BAC的平分线(保留作图痕迹,不写作法). 
(1)如图1,P是BC边的中点;
(2)如图2,直线l与⊙O相切于点P,且l∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解当地气温变化情况,某研究小组记录了寒假期间连续6天的最高气温,结果如下(单位:℃):﹣6,﹣3,x,2,﹣1,3,若这组数据的中位数是﹣1,在下列结论中:①方差是8;②极差是9;③众数是﹣1;④平均数是﹣1,其中正确的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].
(1)如图①,对△ABC作变换[60°, ![]() ]得△AB′C′,则S△AB′C′:S△ABC=;直线BC与直线B′C′所夹的锐角为度;
]得△AB′C′,则S△AB′C′:S△ABC=;直线BC与直线B′C′所夹的锐角为度; 
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB′C′,使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值; 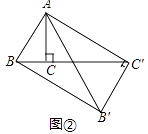
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,求θ和n的值. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE= ![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是(填序号)
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是(填序号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AB=BC=2 ![]() ,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )
,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( ) 
A.2
B.![]()
C.![]()
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com