
分析 (1)用代入法,把②式变成y=2x-4,代入①式,解一元二次方程即可.
(2)首先利用②-①,③-②即可消去未知数c,即可得到一个关于a,b的方程组,求得a,b的值,然后代入①即可求得c的值.
解答 解:(1)解方程组$\left\{\begin{array}{l}{3x+\frac{1}{2}y=10①}\\{2x-y=4②}\end{array}\right.$
由②得:y=2x-4③,
把③代入①,整理得:4x-2=10,解得:x=3.
把x=3代入③得y=2.
∴原方程的解为:$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$.
(2)$\left\{\begin{array}{l}{a-b+c=6①}\\{4a+2b+c=3②}\\{9a-3b+c=18③}\end{array}\right.$
②-①得3a+3b=-3,
③-②得5a-5b=15,
整理得$\left\{\begin{array}{l}{a+b=-1}\\{a-b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$,
把a=1,b=-2代入方程①得:1+2+c=5
解得:c=3.
则方程组的解是:$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=3}\end{array}\right.$.
点评 本题考查的是二元一次方程组、三元一次方程组的解法,利用了消元的思想,消元的方法有:代入消元法与加减消元法..


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
| 科目 | 语文 | 数学 | 英语 |
| 得分 | 120 | 146 | 140 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
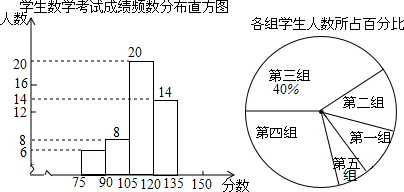
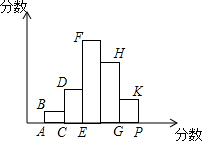 如图所示,根据某班54个学生的数学成绩绘制的频数分布直方图中,各小长方形的高的比AB:CD:EF:GH:PK=1:3:7:5:2,若后两组为80分以上学生数,则80分以上学生人数是21.
如图所示,根据某班54个学生的数学成绩绘制的频数分布直方图中,各小长方形的高的比AB:CD:EF:GH:PK=1:3:7:5:2,若后两组为80分以上学生数,则80分以上学生人数是21.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好得了解本次大赛的成绩分布情况,随机抽取了200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好得了解本次大赛的成绩分布情况,随机抽取了200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:| 成绩x/分 | 频数 | 频率 |
| 50≤x<60 | 10 | 0.05 |
| 60≤x<70 | 20 | 0.10 |
| 70≤x<80 | 30 | b |
| 80≤x<90 | a | 0.30 |
| 90≤x≤100 | 80 | 0.40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com