
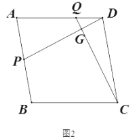
【题目】已知四边形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 、
、![]() 边上的点,
边上的点,![]() 与
与![]() 交于点
交于点![]() .
.
(1)如图1,若四边形![]() 是正方形,且
是正方形,且![]() ,求证:
,求证:![]() ;
;
(2)如图2,若四边形![]() 是菱形,试探究当
是菱形,试探究当![]() 与
与![]() 满足什么关系,使得
满足什么关系,使得![]() ;
;
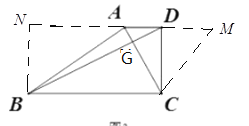
(3)如图3,![]() ,
,![]() ,
,![]() ,试判断
,试判断![]() 与
与![]() 的数量关系,请说明理由.
的数量关系,请说明理由.


【答案】(1)见解析.(2)满足![]() +
+![]()
![]() 时,
时,![]() ,理由见解析.
,理由见解析.
(3)![]() ,理由见解析.
,理由见解析.
【解析】
(1)由四边形ABCD为正方形,利用正方形的性质得到一对角为直角,相等,且AD=DC,利用同角的余角相等得到一对角相等,利用AAS得到三角形ADP与三角形DCQ全等,利用全等三角形对应边相等即可得证;(2)满足![]() +
+![]()
![]() 时,
时,![]() ,在AD的延长线上取点M,使CM=CQ,利用平行线的性质,以及同角(或等角)的补角相等得到三角形ADP与三角形DCM相似,利用相似三角形对应边成比例即可得证.(3)由(2)问的启示,构建出相同情境下的图形,把
,在AD的延长线上取点M,使CM=CQ,利用平行线的性质,以及同角(或等角)的补角相等得到三角形ADP与三角形DCM相似,利用相似三角形对应边成比例即可得证.(3)由(2)问的启示,构建出相同情境下的图形,把![]() 转化到(2)中角的已知条件上,利用同位置的相似三角形可得结论.
转化到(2)中角的已知条件上,利用同位置的相似三角形可得结论.
(1)证明:∵四边形ABCD是正方形, ∴∠A=∠ADC=90°,AD=DC,
∴∠ADP+∠APD=90°, ∵DP⊥CQ, ∴∠ADP+∠CQD=90°, ∴∠APD=∠CQD,
∴△ADP≌△DCQ, ∴DP=CQ;
(2)满足![]() +
+![]()
![]() 时,
时,![]() .
.
理由如下:如图,延长AD至M,使CM=CQ,则![]() ,
,
∵AB∥CD, ∴∠A=∠CDM,
![]()
![]() ,
,
∵AD∥BC, ∴∠B+∠A=180°,∴∠QGP+∠A=180°,
∴∠APD=∠CQM=∠CMQ,
∴△ADP∽△DCM,
∴ ![]() ,
,
![]()
![]() .
.

(3)![]() ,理由如下:
,理由如下:
如图,AC与BD相交于G,延长DA至N,使BC=DN,又![]() ,
,
所以四边形BNDC为平行四边形,所以![]()
因为![]() ,
,![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() .
.
延长AD至M,使CM=CA,
结合(2)得:![]() ,
,
所以:![]() ,因为
,因为![]() ,
,
所以![]() ,所以
,所以![]() .
.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案科目:初中数学 来源: 题型:
【题目】(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y=![]() x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为
x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为![]() m.
m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
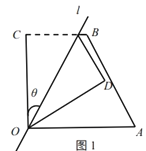
【题目】(阅读)如图1,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,经过点
,经过点![]() 的直线
的直线![]() 将四边形分成两部分,直线
将四边形分成两部分,直线![]() 与
与![]() 所成的角设为
所成的角设为![]() ,将四边形
,将四边形![]() 的直角
的直角![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,我们把这个操作过程记为
处,我们把这个操作过程记为![]() .
.
(理解)若点![]() 与点
与点![]() 重合,则这个操作过程为
重合,则这个操作过程为![]() [__________,__________];
[__________,__________];
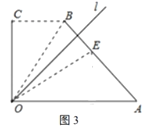
(尝试)
(1)若点![]() 恰为
恰为![]() 的中点(如图2),求
的中点(如图2),求![]() ;
;
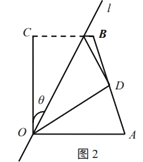
(2)经过![]() 操作,点
操作,点![]() 落在
落在![]() 处,若点
处,若点![]() 在四边形
在四边形![]() 的边
的边![]() 上(如图3),求出
上(如图3),求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,如果点
中,如果点![]() ,点
,点![]() 为某个菱形的一组对角的顶点,且点
为某个菱形的一组对角的顶点,且点![]() 在直线
在直线![]() 上,那么称该菱形为点
上,那么称该菱形为点![]() 的“伴随菱形”,下图为点
的“伴随菱形”,下图为点![]() 的“伴随菱形”的一个示意图.
的“伴随菱形”的一个示意图.
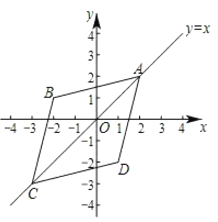
已知点![]() 的坐标为(1,1),点
的坐标为(1,1),点![]() 的坐标为
的坐标为![]() .
.
(1)点![]() 中,能够成为点
中,能够成为点![]() 的“伴随菱形”的顶点的是__________________;
的“伴随菱形”的顶点的是__________________;
(2)如果四边形![]() 是点
是点![]() 的“伴随菱形”.
的“伴随菱形”.
①当点![]() 的坐标为
的坐标为![]() 时,求四边形
时,求四边形![]() 的面积;
的面积;
②当四边形![]() 中较小内角的度数为60°时,求四边形
中较小内角的度数为60°时,求四边形![]() 的面积;
的面积;
③当四边形![]() 的面积为8,且与直线
的面积为8,且与直线![]() 有公共点时,直接写出
有公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
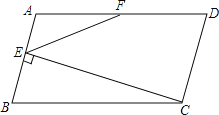
【题目】如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).
(1)当α=60°时,求CE的长;
(2)当60°<α<90°时,
①是否存在正整数k,使得∠EFD=k∠AEF?若存在,求出k的值;若不存在,请说明理由.
②连接CF,当CE2﹣CF2取最大值时,求tan∠DCF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
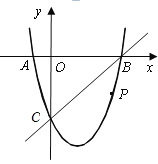
(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形![]() .是否存在点P,使四边形
.是否存在点P,使四边形![]() 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
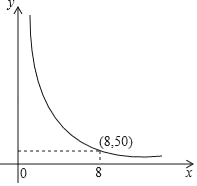
【题目】码头工人每天往一艘轮船上装载货物,平均每天装载速度y(吨/元)与装完货物所需时间x(天)之间是反比例函数关系,其图象如图所示.
(1)求这个反比例函数的表达式;
(2)由于紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸货多少吨?
(3)若码头原有工人10名,且每名工人每天的装卸量相同,装载完毕恰好用了8天时间,在(2)的条件下,至少需要增加多少名工人才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,M、N是BD的三等分点,连接CM并延长交AB于点E,连接EN并延长交CD于点F,以下结论:
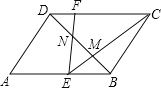
①E为AB的中点;
②FC=4DF;
③S△ECF=![]() ;
;
④当CE⊥BD时,△DFN是等腰三角形.
其中一定正确的是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com