
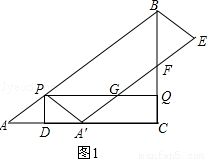
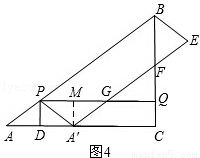
ШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=8cmЃЌAB=10cmЃЎЕуPДгЕуAГіЗЂЃЌвд5cm/sЕФЫйЖШДгЕуAдЫЖЏЕНжеЕуBЃЛЭЌЪБЃЌЕуQДгЕуCГіЗЂЃЌвд3cm/sЕФЫйЖШДгЕуCдЫЖЏЕНжеЕуBЃЌСЌНсPQЃЛЙ§ЕуPзїPDЁЭACНЛACгкЕуDЃЌНЋЁїAPDбиPDЗелЕУЕНЁїAЁфPDЃЌвдAЁфPКЭPBЮЊСкБпзї?AЁфPBEЃЌAЁфEНЛЩфЯпBCгкЕуFЃЌНЛЩфЯпPQгкЕуGЃЎЩш?AЁфPBEгыЫФБпаЮPDCQжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊScm2ЃЌЕуPЕФдЫЖЏЪБМфЮЊtsЃЎ
ЃЈ1ЃЉЕБtЮЊКЮжЕЪБЃЌЕуAЁфгыЕуCжиКЯЃЛ
ЃЈ2ЃЉгУКЌtЕФДњЪ§ЪНБэЪОQFЕФГЄЃЛ
ЃЈ3ЃЉЧѓSгыtЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ4ЃЉЧыжБНгаДГіЕБЩфЯпPQНЋ?AЁфPBEЗжГЩЕФСНВПЗжЭМаЮЕФУцЛ§жЎБШЪЧ1ЃК3ЪБtЕФжЕЃЎ

ЃЈ1ЃЉt=1ЃЈ2ЃЉЕБ0ЃМtЁм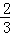 ЪБЃЌQF=6Љ9tЃЛЕБ
ЪБЃЌQF=6Љ9tЃЛЕБ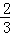 ЃМtЃМ2ЪБЃЌQF=9tЉ6ЃЎ
ЃМtЃМ2ЪБЃЌQF=9tЉ6ЃЎ
ЕБ0ЃМtЁм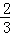 ЪБЃЌS=12t2ЃЛЕБ
ЪБЃЌS=12t2ЃЛЕБ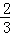 ЃМtЁм1ЪБЃЌS=Љ42t2+72tЉ24ЃКЕБ1ЃМtЃМ2ЪБЃЌS=6t2Љ24t+24ЃЎ
ЃМtЁм1ЪБЃЌS=Љ42t2+72tЉ24ЃКЕБ1ЃМtЃМ2ЪБЃЌS=6t2Љ24t+24ЃЎ
tЕФжЕЮЊ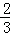 УыЛђ
УыЛђ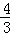 УыЃЎ
УыЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉвзжЄЁїADPЁзЁїACBЃЌДгЖјПЩЕУAD=4tЃЌгЩелЕўПЩЕУAAЁф=2AD=8tЃЌгЩЕуAЁфгыЕуCжиКЯПЩЕУ8t=8ЃЌДгЖјПЩвдЧѓГіtЕФжЕЃЎ
ЃЈ2ЃЉИљОнЕуFЕФЮЛжУВЛЭЌЃЌПЩЗжЕуFдкBQЩЯЃЈВЛАќРЈЕуBЃЉЁЂдкCQЩЯЃЈВЛАќРЈЕуQЃЉЁЂдкBCЕФбгГЄЯпЩЯШ§жжЧщПіНјааЬжТлЃЌОЭПЩНтОіЮЪЬтЃЎ
ЃЈ3ЃЉИљОнЕуFЕФЮЛжУВЛЭЌЃЌПЩЗжЕуFдкBQЩЯЃЈВЛАќРЈЕуBЃЉЁЂдкCQЩЯЃЈВЛАќРЈЕуQЃЉЁЂдкBCЕФбгГЄЯпЩЯШ§жжЧщПіНјааЬжТлЃЌОЭПЩНтОіЮЪЬтЃЎ
ЃЈ4ЃЉПЩЗжЂйSЁїAЁфPGЃКSЫФБпаЮPBEG=1ЃК3ЃЌШчЭМ7ЃЌЂкSЁїBPNЃКSЫФБпаЮPNEAЁф=1ЃК3ЃЌШчЭМ8ЃЌСНжжЧщПіНјааЬжТлЃЌОЭПЩНтОіЮЪЬтЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉШчЭМ1ЃЌ
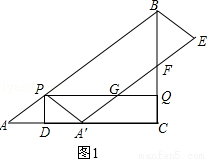
гЩЬтПЩЕУЃКPAЁф=PA=5tЃЌCQ=3tЃЌAD=AЁфDЃЎ
ЁпЁЯACB=90ЁуЃЌAC=8ЃЌAB=10ЃЌЁрBC=6ЃЎ
ЁпЁЯADP=ЁЯACB=90ЁуЃЌ
ЁрPDЁЮBCЃЎ
ЁрЁїADPЁзЁїACBЃЎ
Ёр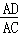 =
=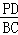 =
= ЃЎ
ЃЎ
Ёр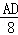 =
=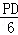 =
=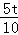 ЃЎ
ЃЎ
ЁрAD=4tЃЌPD=3tЃЎ
ЁрAAЁф=2AD=8tЃЎ
ЕБЕуAЁфгыЕуCжиКЯЪБЃЌAAЁф=ACЃЎ
Ёр8t=8ЃЎ
Ёрt=1ЃЎ
ЃЈ2ЃЉЂйЕБЕуFдкЯпЖЮBQЩЯЃЈВЛАќРЈЕуBЃЉЪБЃЌШчЭМ1ЃЌ
дђгаCQЁмCFЃМCBЃЎ
ЁпЫФБпаЮAЁфPBEЪЧЦНааЫФБпаЮЃЌ
ЁрAЁфEЁЮBPЃЎ
ЁрЁїCAЁфFЁзЁїCABЃЎ
Ёр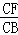 =
=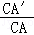 ЃЎ
ЃЎ
Ёр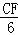 =
=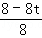 ЃЎ
ЃЎ
ЁрCF=6Љ6tЃЎ
Ёр3tЁм6Љ6tЃМ6ЃЎ
Ёр0ЃМtЁм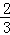 ЃЎ
ЃЎ
ДЫЪБQF=CFЉCQ=6Љ6tЉ3t=6Љ9tЃЎ
ЂкЕБЕуFдкЯпЖЮCQЩЯЃЈВЛАќРЈЕуQЃЉЪБЃЌШчЭМ2ЃЌ
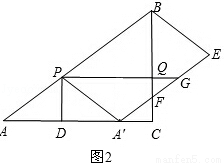
дђга0ЁмCFЃМCQЃЎ
ЁпCF=6Љ6tЃЌCQ=3tЃЌ
Ёр0Ём6Љ6tЃМ3tЃЎ
Ёр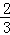 ЃМtЁм1ЃЎ
ЃМtЁм1ЃЎ
ДЫЪБQF=CQЉCF=3tЉЃЈ6Љ6tЃЉ=9tЉ6ЃЎ
ЂлЕБЕуFдкЯпЖЮBCЕФбгГЄЯпЩЯЪБЃЌШчЭМ3ЃЌ
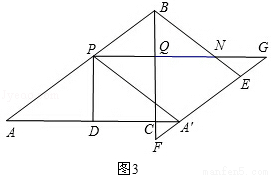
дђгаAAЁфЃОACЃЌЧвAPЃМABЃЎ
Ёр8tЃО8ЃЌЧв5tЃМ10ЃЎ
Ёр1ЃМtЃМ2ЃЎ
ЭЌРэПЩЕУЃКCF=6tЉ6ЃЎ
ДЫЪБQF=QC+CF=3t+6tЉ6=9tЉ6ЃЎ
злЩЯЫљЪіЃКЕБ0ЃМtЁм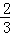 ЪБЃЌQF=6Љ9tЃЛЕБ
ЪБЃЌQF=6Љ9tЃЛЕБ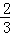 ЃМtЃМ2ЪБЃЌQF=9tЉ6ЃЎ
ЃМtЃМ2ЪБЃЌQF=9tЉ6ЃЎ
ЃЈ3ЃЉЂйЕБ0ЃМtЁм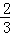 ЪБЃЌ
ЪБЃЌ
Й§Еу AЁфзїAЁфMЁЭPGЃЌДЙзуЮЊMЃЌШчЭМ4ЃЌ
дђгаAЁфM=CQ=3tЃЎ
Ёп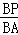 =
=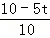 =
=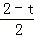 ЃЌ
ЃЌ =
=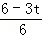 =
=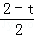 ЃЌ
ЃЌ
Ёр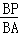 =
=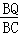 ЃЌ
ЃЌ
ЁпЁЯPBQ=ЁЯABCЃЌ
ЁрЁїBPQЁзЁїBACЃЎ
ЁрЁЯBQP=ЁЯBCAЃЎ
ЁрPQЁЮACЃЎ
ЁпAPЁЮAЁфGЃЎ
ЁрЫФБпаЮAPGAЁфЪЧЦНааЫФБпаЮЃЎ
ЁрPG=AAЁф=8tЃЎ
ЁрS=SЁїAЁфPG=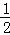 PG•AЁфM
PG•AЁфM
=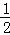 ЁС8tЁС3t=12t2ЃЎ
ЁС8tЁС3t=12t2ЃЎ
ЂкЕБ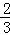 ЃМtЁм1ЪБЃЌ
ЃМtЁм1ЪБЃЌ
Й§Еу AЁфзїAЁфMЁЭPGЃЌДЙзуЮЊMЃЌШчЭМ5ЃЌ
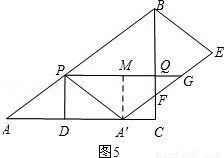
дђгаAЁфM=QC=3tЃЌPQ=DC=8Љ4tЃЌPG=AAЁф=8tЃЌQG=PGЉPQ=12tЉ8ЃЌQF=9tЉ6ЃЎЃЎ
ЁрS=SЁїAЁфPGЉSЁїGQF
=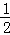 PG•AЁфMЉ
PG•AЁфMЉ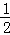 QG•QF
QG•QF
=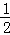 ЁС8tЁС3tЉ
ЁС8tЁС3tЉ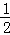 ЁСЃЈ12tЉ8ЃЉЁСЃЈ9tЉ6ЃЉ
ЁСЃЈ12tЉ8ЃЉЁСЃЈ9tЉ6ЃЉ
=Љ42t2+72tЉ24ЃЎ
ЂлЕБ1ЃМtЃМ2ЪБЃЌШчЭМ6ЃЌ
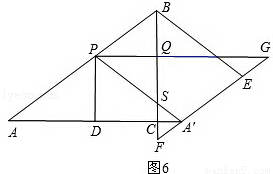
ЁпPQЁЮACЃЌPA=PAЁф
ЁрЁЯBPQ=ЁЯPAAЁфЃЌЁЯQPAЁф=ЁЯPAЁфAЃЌЁЯPAAЁф=ЁЯPAЁфAЃЎ
ЁрЁЯBPQ=ЁЯQPAЁфЃЎ
ЁпЁЯPQB=ЁЯPQS=90ЁуЃЌ
ЁрЁЯPBQ=ЁЯPSQЃЎ
ЁрPB=PSЃЎ
ЁрBQ=SQЃЎ
ЁрSQ=6Љ3tЃЎ
ЁрS=SЁїPQS= PQ•QS=
PQ•QS= ЁСЃЈ8Љ4tЃЉЁСЃЈ6Љ3tЃЉ=6t2Љ24t+24ЃЎ
ЁСЃЈ8Љ4tЃЉЁСЃЈ6Љ3tЃЉ=6t2Љ24t+24ЃЎ
злЩЯЫљЪіЃКЕБ0ЃМtЁм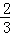 ЪБЃЌS=12t2ЃЛЕБ
ЪБЃЌS=12t2ЃЛЕБ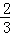 ЃМtЁм1ЪБЃЌS=Љ42t2+72tЉ24ЃКЕБ1ЃМtЃМ2ЪБЃЌS=6t2Љ24t+24ЃЎ
ЃМtЁм1ЪБЃЌS=Љ42t2+72tЉ24ЃКЕБ1ЃМtЃМ2ЪБЃЌS=6t2Љ24t+24ЃЎ
ЃЈ4ЃЉЂйШєSЁїAЁфPGЃКSЫФБпаЮPBEG=1ЃК3ЃЌ
Й§ЕуAЁфзїAЁфMЁЭPGЃЌДЙзуЮЊMЃЌЙ§ЕуAЁфзїAЁфTЁЭPBЃЌДЙзуЮЊTЃЌШчЭМ7ЃЌ
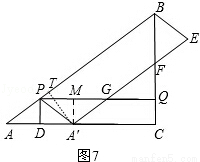
дђгаAЁфM=PD=QC=3tЃЌPG=AAЁф=8tЃЎ
ЁрSЁїAЁфPG= ЁС8tЁС3t=12t2ЃЎ
ЁС8tЁС3t=12t2ЃЎ
ЁпSЁїAPAЁф= AP•AЁфT=
AP•AЁфT= AAЁф•PDЃЌ
AAЁф•PDЃЌ
ЁрAЁфT=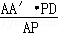 =
=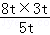 =
=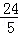 tЃЎ
tЃЎ
ЁрS?PBEAЁф=PB•AЁфT=ЃЈ10Љ5tЃЉЁС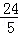 t=24tЃЈ2ЉtЃЉЃЎ
t=24tЃЈ2ЉtЃЉЃЎ
ЁпSЁїAЁфPGЃКSЫФБпаЮPBEG=1ЃК3ЃЌ
ЁрSЁїAЁфPG=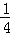 ЁСS?PBEAЁфЃЎ
ЁСS?PBEAЁфЃЎ
Ёр12t2=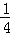 ЁС24tЃЈ2ЉtЃЉЃЎ
ЁС24tЃЈ2ЉtЃЉЃЎ
ЁпtЃО0ЃЌ
Ёрt=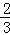 ЃЎ
ЃЎ
ЂкШєSЁїBPNЃКSЫФБпаЮPNEAЁф=1ЃК3ЃЌШчЭМ8ЃЌ

ЭЌРэПЩЕУЃКЁЯBPQ=ЁЯAЁфPQЃЌBQ=6Љ3tЃЌPQ=8Љ4tЃЌS?PBEAЁф=24tЃЈ2ЉtЃЉЃЎ
ЁпЫФБпаЮPBEAЁфЪЧЦНааЫФБпаЮЃЌ
ЁрBEЁЮPAЁфЃЎ
ЁрЁЯBNP=ЁЯNPAЁфЃЎ
ЁрЁЯBPN=ЁЯBNPЃЎ
ЁрBP=BNЃЎ
ЁпЁЯBQP=ЁЯBQN=90ЁуЃЌ
ЁрPQ=NQЃЎ
ЁрSЁїBPN= PN•BQ=PQ•BQ
PN•BQ=PQ•BQ
=ЃЈ8Љ4tЃЉЁСЃЈ6Љ3tЃЉЃЎ
ЁпSЁїBPNЃКSЫФБпаЮPNEAЁф=1ЃК3ЃЌ
ЁрSЁїBPN=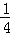 ЁСS?PBEAЁфЃЎ
ЁСS?PBEAЁфЃЎ
ЁрЃЈ8Љ4tЃЉЁСЃЈ6Љ3tЃЉ=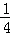 ЁС24tЃЈ2ЉtЃЉЃЎ
ЁС24tЃЈ2ЉtЃЉЃЎ
ЁпtЃМ2ЃЌ
Ёрt=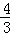 ЃЎ
ЃЎ
злЩЯЫљЪіЃКЕБЩфЯпPQНЋ?AЁфPBEЗжГЩЕФСНВПЗжЭМаЮЕФУцЛ§жЎБШЪЧ1ЃК3ЪБЃЌtЕФжЕЮЊ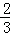 УыЛђ
УыЛђ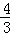 УыЃЎ
УыЃЎ
ПМЕуЃКЯрЫЦаЮзлКЯЬтЃЛНтвЛдЊвЛДЮВЛЕШЪНзщЃЛЕШбќШ§НЧаЮЕФХаЖЈгыаджЪЃЛЙДЙЩЖЈРэЃЛЦНааЫФБпаЮЕФаджЪЃЛЯрЫЦШ§НЧаЮЕФХаЖЈгыаджЪЃЎнМгХЭјАцШЈЫљга


 аТЫМЮЌКЎМйзївЕЯЕСаД№АИ
аТЫМЮЌКЎМйзївЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2013-2014бЇФъАВЛеЪЎДѓУћаЃОХФъМЖЕкЫФДЮдТПМЪ§бЇЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
ЧхУїНкЧАЃЌФГАрЗжГЩМзЁЂввСНзщШЅОрРыбЇаЃ4kmЕФСвЪПСъдАЩЈФЙЃЎМззщВНааЃЌввзщЦяздааГЕЃЌЫћУЧЭЌЪБДгбЇаЃГіЗЂЃЌНсЙћввзщБШМззщдч20minЕНДяФПЕФЕиЃЎвбжЊЦяздааГЕЕФЫйЖШЪЧВНааЫйЖШЕФ2БЖЃЌЪдЧѓВНааЕФЫйЖШ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2013-2014бЇФъЫФДЈЪЁУМЩНЪаЛЊаЫСЊвъбЇаЃОХФъМЖЯТбЇЦкЦкжаПМЪдЪ§бЇЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
2010ФъФГОАЧјШЋФъгЮПЭШЫЪ§ГЌ8030000ШЫДЮЃЌ8030000гУПЦбЇМЦЪ§ЗЈБэЪОЪЧЃЈ ЃЉ
AЁЂ803ЁС104 BЁЂ80.3ЁС105 CЁЂ8.03ЁС106 DЁЂ8.03ЁС107
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2013-2014бЇФъЫФДЈЪЁРжЩНЪаМаНЯиОХФъМЖБЯвЕЛсПМЪЪгІадПМЪдЪ§бЇЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКЬюПеЬт
ЛЏМђДњЪ§ЪН ЫљЕУЕФНсЙћЪЧ ЃЎ
ЫљЕУЕФНсЙћЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2013-2014бЇФъЫФДЈЪЁРжЩНЪаМаНЯиОХФъМЖБЯвЕЛсПМЪЪгІадПМЪдЪ§бЇЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
ШчБэЪЧЮвЪа11ИіЧјЯиШЅФъ5дТ1ШезюИпЦјЮТЃЈЁцЃЉЕФЭГМЦНсЙћЃК
ЪажаЧј | ЖыУМЩНЪа | ЩГЭхЧј | ЮхЭЈЧХЧј | Н№ПкКгЧј | ъљЮЊЯи | ОЎбаЯи | МаНЯи | ухДЈЯи | ЖыБпЯи | ТэБпЯи |
26 | 25 | 29 | 26 | 28 | 26 | 26 | 27 | 25 | 28 | 25 |
ИУШезюИпЦјЮТЕФжкЪ§КЭжаЮЛЪ§ЗжБ№ЪЧЃЈЁЁЁЁЃЉЃЎ
AЃЎ25ЁцЃЌ26Ёц BЃЎ26ЁцЃЌ26Ёц
CЃЎ25ЁцЃЌ25Ёц DЃЎ26ЁцЃЌ27Ёц
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2013-2014бЇФъМЊСжЪЁГЄДКЪаГЏбєЧјжаПМвЛФЃЪ§бЇЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
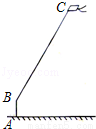
жмФЉЃЌаЁЧПдкЮФЛЏЙуГЁЗХЗчѓнЃЎШчЭМЃЌаЁЧПЮЊСЫМЦЫуЗчѓнРыЕиУцЕФИпЖШЃЌЫћВтЕУЗчѓнЕФбіНЧЮЊ58ЁуЃЌвбжЊЗчѓнЯпBCЕФГЄЮЊ10УзЃЌаЁЧПЕФЩэИпABЮЊ1.55УзЃЎЧыФуАяаЁЧПЛГіВтСПЪОвтЭМЃЌВЂМЦЫуГіЗчѓнРыЕиУцЕФИпЖШЃЈНсЙћОЋШЗЕН0.1УзЃЉЃЎЃЈВЮПМЪ§ОнЃКsin58Ёу=0.85ЃЌcos58Ёу=0.53ЃЌtan58Ёу=1.60ЃЉ
 ]
]
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2013-2014бЇФъМЊСжЪЁГЄДКЪаГЏбєЧјжаПМвЛФЃЪ§бЇЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКЬюПеЬт
ШчЭМЃЌMNЪЧЁбOЕФжБОЖЃЌОиаЮABCDЕФЖЅЕуAЁЂDдкMNЩЯЃЌЖЅЕуBЁЂCдкЁбOЩЯЃЌШєЁбOЕФАыОЖЮЊ5ЃЌAB=4ЃЌдђADБпЕФГЄЮЊЁЁЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2013-2014бЇФъББОЉЪаЫГвхЧјжаПМЖўФЃЪ§бЇЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
БЃеЯЗПНЈЩшЪЧУёаФЙЄГЬЃЌФГЪаДг2009ФъМгПьБЃеЯЗПНЈЩшЙЄГЬЃЎЯжЭГМЦСЫИУЪаДг2009ФъЕН2013Фъет5ФъаТНЈБЃеЯЗПЧщПіЃЌЛцжЦГЩШчЭМ1ЁЂ2ЫљЪОЕФелЯпЭГМЦЭМКЭВЛЭъећЕФЬѕаЮЭГМЦЭМЃЎ

ЃЈ1ЃЉаЁгБПДСЫЭГМЦЭМКѓЫЕЃКЁАИУЪа2012ФъаТНЈБЃеЯЗПЕФЬзЪ§БШ2011ФъЩйСЫЃЎЁБФуШЯЮЊаЁгБЕФЫЕЗЈе§ШЗТ№ЃПЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЧѓ2012ФъаТНЈБЃеЯЗПЕФЬзЪ§ЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉЧѓет5ФъЦНОљУПФъаТНЈБЃеЯЗПЕФЬзЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2013-2014бЇФъББОЉЪаЫГвхЧјжаПМвЛФЃЪ§бЇЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
ШєвЛИіЖрБпаЮЕФУПвЛИіЭтНЧЖМЪЧ40ЁуЃЌдђетИіЖрБпаЮЪЧЃЈ ЃЉ
AЃЎСљБпаЮ BЃЎАЫБпаЮ CЃЎОХБпаЮ DЃЎЪЎБпаЮ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com