
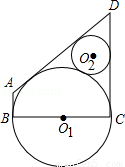
如图,以BC为直径的⊙O1与⊙O2外切,⊙O1与⊙O2的外公切线交于点D,且∠ADC=60°,过B点的⊙O1的切线交其中一条外公切线于点A.若⊙O2的面积为π,则四边形ABCD的面积是 .
12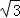
【解析】解:∵⊙O2的面积为π,
∴⊙O2的半径是1,
∵AB和AH是⊙O1的切线,
∴AB=AH,
设⊙O2的半径是R,
连接DO2,DO1,O2E,O1H,AO1,作O2F⊥BC于F,
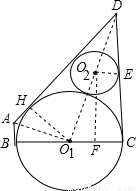
∵⊙O1与⊙O2外切,⊙O1与⊙O2的外公切线DC.DA,∠ADC=60°,
∴D.O2、O1三点共线,∠CDO1=30°,
∴∠DAO1=60°,∠O2EC=∠ECF=∠CFO2=90°,
∴四边形CFO2E是矩形,
∴O2E=CF,CE=FO2,∠FO2O1=∠CDO1=30°,
∴DO2=2O2E=2,∠HAO1=60°,R+1=2(R﹣1),
解得:R=3,
即DO1=2+1+3=6,
在Rt△CDO1中,由勾股定理得:CD=3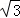 ,
,
∵∠HO1A=90°﹣60°=30°,HO1=3,
∴AH=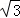 =AB,
=AB,
∴四边形ABCD的面积是: ×(AB+CD)×BC=
×(AB+CD)×BC= ×(
×(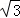 +3
+3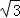 )×(3+3)=12
)×(3+3)=12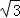 .
.


科目:初中数学 来源: 题型:
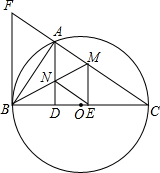 如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF•AC,cos∠ABD=
如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF•AC,cos∠ABD=| 3 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•浦口区一模)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=70°,BC=2,则图中阴影部分面积为
(2012•浦口区一模)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=70°,BC=2,则图中阴影部分面积为| 7 |
| 18 |
| 7 |
| 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:
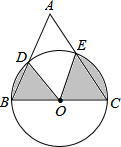 (2013•眉山)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=60°,BC=4,则图中阴影部分的面积为
(2013•眉山)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=60°,BC=4,则图中阴影部分的面积为| 4 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•攀枝花)如图,以BC为直径的⊙O1与⊙O2外切,⊙O1与⊙O2的外公切线交于点D,且∠ADC=60°,过B点的⊙O1的切线交其中一条外公切线于点A.若⊙O2的面积为π,则四边形ABCD的面积是
(2012•攀枝花)如图,以BC为直径的⊙O1与⊙O2外切,⊙O1与⊙O2的外公切线交于点D,且∠ADC=60°,过B点的⊙O1的切线交其中一条外公切线于点A.若⊙O2的面积为π,则四边形ABCD的面积是| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com