Question

17．如图，在△ABC中，AB=AC，AD⊥BC于点D，BC=10cm，AD=8cm．点P从点B出发，在线段BC上以每秒3cm的速度向点C匀速运动，与此同时，垂直于AD的直线m从底边BC出发，以每秒2cm的速度沿DA方向匀速平移，分别交AB、AC、AD于E、F、H，当点P到达点C时，点P与直线m同时停止运动，设运动时间为t秒（t＞0）．
（1）当t=2时，连接DE、DF，求证：四边形AEDF为菱形；
（2）在整个运动过程中，问所形成的△PEF是否存在最大面积；如果存在请求出，如果不存在说明理由．
（3）是否存在某一时刻t，使△PEF为直角三角形？若存在，请求出此时刻t的值；若不存在，请说明理由．

Answer 1

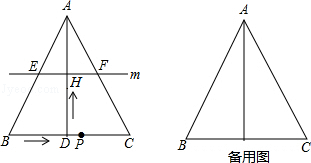
分析 （1）如答图1所示，利用菱形的定义证明；
（2）如答图2所示，首先求出△PEF的面积的表达式，然后利用二次函数的性质求解；
（3）如答图3所示，分三种情形，需要分类讨论，分别求解．

解答 （1）证明：当t=2时，DH=AH=4，则H为AD的中点，如答图1所示．
又∵EF⊥AD，
∴EF为AD的垂直平分线，
∴AE=DE，AF=DF．
∵AB=AC，AD⊥BC于点D，
∴AD⊥BC，∠B=∠C．
∴EF∥BC，
∴∠AEF=∠B，∠AFE=∠C，
∴∠AEF=∠AFE，
∴AE=AF，
∴AE=AF=DE=DF，即四边形AEDF为菱形．

（2）解：如答图2所示，由（1）知EF∥BC，
∴△AEF∽△ABC，
∴$\frac{EF}{BC}=\frac{AH}{AD}$，即 $\frac{EF}{10}=\frac{8-2t}{8}$，解得：EF=10-$\frac{5}{2}$t．
S_△PEF=$\frac{1}{2}$EF•DH=$\frac{1}{2}$（10-$\frac{5}{2}$t）•2t=-$\frac{5}{2}$t²+10t=-$\frac{5}{2}$（t-2）²+10（0＜t＜$\frac{10}{3}$），
∴当t=2秒时，S_△PEF存在最大值，最大值为10cm²．
（3）解：存在．理由如下：
①若点E为直角顶点，如答图3①所示，
此时PE∥AD，PE=DH=2t，BP=3t．
∵PE∥AD，
∴$\frac{PE}{AD}=\frac{BP}{BD}$，
即 $\frac{2t}{8}=\frac{3t}{5}$，
∴t=0（舍），故此种情形不存在；
②若点F为直角顶点，如答图3②所示，
此时PF∥AD，PF=DH=2t，BP=3t，CP=10-3t．
∵PF∥AD，∴$\frac{PF}{AD}=\frac{CP}{CD}$，即 $\frac{2t}{8}=\frac{10-3t}{5}$，解得t=$\frac{40}{17}$；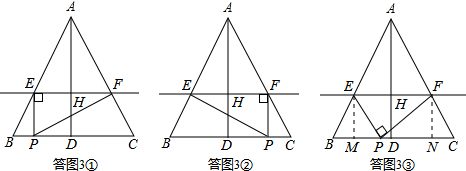

③若点P为直角顶点，如答图3③所示．
过点E作EM⊥BC于点M，过点F作FN⊥BC于点N，则EM=FN=DH=2t，EM∥FN∥AD．
∵EM∥AD，
∴$\frac{EM}{AD}=\frac{BM}{BD}$，
即 $\frac{2t}{8}=\frac{BM}{5}$，
解得BM=$\frac{5}{4}$t，
∴PM=BP-BM=3t-$\frac{5}{4}$t=$\frac{7}{4}$t．
在Rt△EMP中，由勾股定理得：PE²=EM²+PM²=（2t）²+（ $\frac{7}{4}$t）²=$\frac{113}{16}$t²．
∵FN∥AD，
∴$\frac{FN}{AD}=\frac{CN}{CD}$，
即 $\frac{2t}{8}=\frac{CN}{5}$，
解得CN=$\frac{5}{4}$t，
∴PN=BC-BP-CN=10-3t-$\frac{5}{4}$t=10-$\frac{17}{4}$t．
在Rt△FNP中，由勾股定理得：PF²=FN²+PN²=（2t）²+（10-$\frac{17}{4}$t）²=$\frac{353}{16}$t²-85t+100．
在Rt△PEF中，由勾股定理得：EF²=PE²+PF²，
即：（10-$\frac{5}{2}$t）²=（ $\frac{113}{16}$t²）+（ $\frac{353}{16}$t²-85t+100）
化简得：$\frac{183}{8}$t²-35t=0，
解得：t=$\frac{280}{183}$或t=0（舍去）
∴t=$\frac{280}{183}$．
综上所述，当t=$\frac{40}{17}$秒或t=$\frac{280}{183}$秒时，△PEF为直角三角形．

点评 此题是四边形综合题，涉及动点与动线两种运动类型．菱形的性质，相似三角形的性质和判定、图形面积及二次函数的极值，勾股定理、解方程等知识点，重点考查了分类讨论的数学思想．