
 如图,菱形ABCD的周长为8,对角线AC和BD相交于点O,AC:BD=1:2,则AO:BO=1:2,菱形ABCD的面积S=$\frac{16}{5}$.
如图,菱形ABCD的周长为8,对角线AC和BD相交于点O,AC:BD=1:2,则AO:BO=1:2,菱形ABCD的面积S=$\frac{16}{5}$. 分析 先找出AO,BO的关系,再确定出AB,用勾股定理确定出x的平方,最后用菱形的面积公式即可得出结论.
解答 解:∵四边形ABCD是菱形,
∴AC=2AO,BD=2BO,
∵AC:BD=1:2,
∴AO:BO=1:2;
设AO=x,(x>0)
则BO=2x,
∵菱形ABCD的周长为8,
∴AB=2,AC⊥BD,
在Rt△AOB中,AO2+BO2=AB2,
∴x2+(2x)2=4,
∴x2=$\frac{4}{5}$,
∵AC=2AO=2x,BD=2BO=4x,
∴S菱形ABCD=$\frac{1}{2}$AC×BD=$\frac{1}{2}$×2x×4x=4x2=4×$\frac{4}{5}$=$\frac{16}{5}$,
故答案为:1:2,$\frac{16}{5}$.
点评 此题是菱形的性质,主要考查的菱形的性质,勾股定理,菱形的面积公式,解本题的关键求出x的平方的值.


科目:初中数学 来源: 题型:选择题
| A. | 向上平移5个单位 | B. | 向下平移5个单位 | ||
| C. | 向上平移$\frac{5}{3}$个单位 | D. | 向下平移$\frac{5}{3}$个单位 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
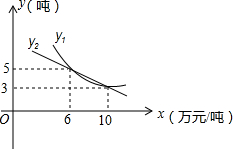 今年某水果超市都以2万元/吨的价格购进甲、乙两种水果,甲水果的销量y1(吨)、乙水果的销量y2(吨)与售价x(万元/吨)之间大致满足如图所示的两个函数关系.
今年某水果超市都以2万元/吨的价格购进甲、乙两种水果,甲水果的销量y1(吨)、乙水果的销量y2(吨)与售价x(万元/吨)之间大致满足如图所示的两个函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
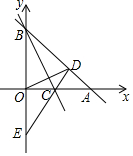 如图,在平面直角坐标系中,直线y=-x+2交x轴于点A,交y轴于点B,C是OA的中点,D为线段AB上一点,且∠ACD=∠BCO.
如图,在平面直角坐标系中,直线y=-x+2交x轴于点A,交y轴于点B,C是OA的中点,D为线段AB上一点,且∠ACD=∠BCO.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
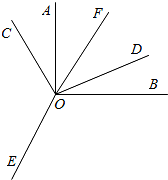 如图,平面内∠AOB=∠COD=90°,∠COE=∠BOE,OF平分∠AOD,则以下结论:
如图,平面内∠AOB=∠COD=90°,∠COE=∠BOE,OF平分∠AOD,则以下结论:| A. | ①②④ | B. | ①②③ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a•b>0,则a>0,b>0 | B. | 若a•b<0,则a<0,b>0 | ||
| C. | 若a•b=0,则a=0且b=0 | D. | 若a•b=0,则a=0或b=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
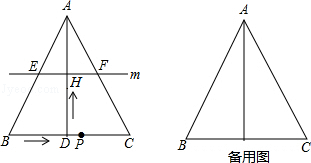
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com