
分析 先根据函数的图象不经过第四象限,舍去不符合题意的数值,再将符合题意的数值代入方程(a-2)x2+ax-1=0中验证,得出符合要求的a的值,然后利用概率公式计算即可求得答案.
解答 解:∵y=2x+a的图象不经过第四象限,
∴a≥0,
∴-1不符合题意,
∵关于x的方程(a-2)x2+ax-1=0有实数根,
∴b2-4ac≥0,
即:a2+4(a-2)≥0.
解得:a≥2$\sqrt{3}$-2或a≤-2$\sqrt{3}$-2,
∴满足条件的a的值有2个,
∴使函数图象不过第四象限,且方程有实根的概率为$\frac{2}{5}$.
故答案为:$\frac{2}{5}$.
点评 本题考查了概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$,关键是求出符合条件的数的个数.同时考查了一次函数图象与系数的关系及根的判别式.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
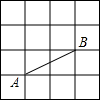 如图是正方形网格,除A,B两点外,在网格的格点上任取一点C,连接AC,BC,能使△ABC为等腰三角形的概率是( )
如图是正方形网格,除A,B两点外,在网格的格点上任取一点C,连接AC,BC,能使△ABC为等腰三角形的概率是( )| A. | $\frac{4}{23}$ | B. | $\frac{6}{23}$ | C. | $\frac{7}{23}$ | D. | $\frac{8}{23}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
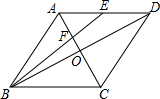 如图,菱形ABCD中,对角线AC与BD交于点O,点E为AD中点,连接BE交AC于点F,则$\frac{AF}{OF}$的值为( )
如图,菱形ABCD中,对角线AC与BD交于点O,点E为AD中点,连接BE交AC于点F,则$\frac{AF}{OF}$的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
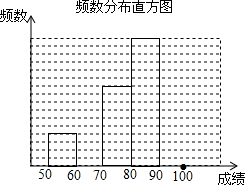 一所中学,为了让学生了解环保知识,增强环保意识,举行了一次环保知识竞赛,共有900名学生参加这次竞赛.为了解本次竞赛的情况,从中抽取了部分学生的成绩(得分均为正整数,满分100分)进行统计.
一所中学,为了让学生了解环保知识,增强环保意识,举行了一次环保知识竞赛,共有900名学生参加这次竞赛.为了解本次竞赛的情况,从中抽取了部分学生的成绩(得分均为正整数,满分100分)进行统计.| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 10 | 0.20 |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100 | m | n |
| 合计 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
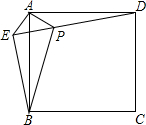 如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于P,若AE=AP=1,PB=$\sqrt{5}$;
如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于P,若AE=AP=1,PB=$\sqrt{5}$;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com