
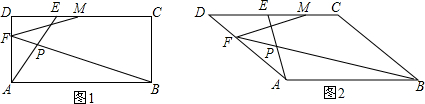
分析 (1)由矩形的性质和勾股定理求出AE,即可得出AP的长;
(2)延长BF、CD交于点N,由矩形的性质得出CN∥AB,得出∠N=∠PBA,∠NEP=∠BAP,由ASA证明△NEP≌△BAP,得出PB=PN,再证出FN=FM,即可得出结论;
(3)延长BF、CD交于点N,由矩形的性质得出CN∥AB,得出∠N=∠PBA,∠NEP=∠BAP,由ASA证明△NEP≌△BAP,得出PB=PN,再证出FN=FM,即可得出结论.
解答 (1)解:∵四边形ABCD为矩形,
∴∠ADE=90°,
∴AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∵点P为线段AE的中点,
∴AP=PE=$\frac{1}{2}$AE=$\frac{1}{2}$×$\sqrt{5}$=$\frac{\sqrt{5}}{2}$;
(2)证明:延长BF、CD交于点N,如图1所示: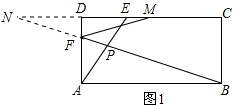 ∵四边形ABCD为矩形,
∵四边形ABCD为矩形,
∴CN∥AB,
∴∠N=∠PBA,∠NEP=∠BAP,
在△NEP和△BAP中,$\left\{\begin{array}{l}{∠NEP=∠BAP}&{\;}\\{AP=PE}&{\;}\\{∠EPN=∠APB}&{\;}\end{array}\right.$,
∴△NEP≌△BAP(ASA),
∴PB=PN,
∵∠DMF=∠ABF,
∴∠N=∠DMF,
∴FN=FM,
∴PB=PN=PF+FN=PF+FM;
(3)解:成立;理由如下:
延长BF、CD交于点N,如图2所示: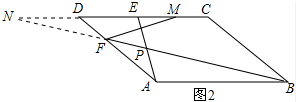 ∵四边形ABCD为矩形,
∵四边形ABCD为矩形,
∴CN∥AB,
∴∠N=∠PBA,∠NEP=∠BAP,
在△NEP和△BAP中,$\left\{\begin{array}{l}{∠NEP=∠BAP}&{\;}\\{AP=PE}&{\;}\\{∠EPN=∠APB}&{\;}\end{array}\right.$,
∴△NEP≌△BAP(ASA),
∴PB=PN,
∵∠DMF=∠ABF,
∴∠N=∠DMF,
∴FN=FM,
∴PB=PN=PF+FN=PF+FM.
点评 本题是四边形综合题目,考查了矩形的性质、平行四边形的性质、全等三角形的判定与性质、等腰三角形的判定等知识;本题综合性强,难度较大,需要通过作辅助线证明三角形全等才能得出结论.


科目:初中数学 来源: 题型:解答题
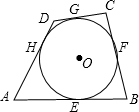 如图,四边形ABCD外切于⊙O,切点分别是E、F、G、H.
如图,四边形ABCD外切于⊙O,切点分别是E、F、G、H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
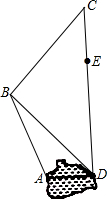 如图是某个园区部分景点(景点A,B,C,D,E)示意图,景点A,D之间是一个荷花池,景点E,D和景点B,D之间正在维修,不能通行.已知AB=400$\sqrt{3}$米,BC=l000米,CE=600米,CD⊥AD,∠BDC=45°,∠ABD=15°.请根据以上条件求出荷花池AD的宽度和景点E,D之间的距离.
如图是某个园区部分景点(景点A,B,C,D,E)示意图,景点A,D之间是一个荷花池,景点E,D和景点B,D之间正在维修,不能通行.已知AB=400$\sqrt{3}$米,BC=l000米,CE=600米,CD⊥AD,∠BDC=45°,∠ABD=15°.请根据以上条件求出荷花池AD的宽度和景点E,D之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
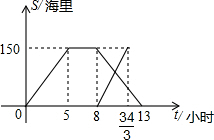 黄岩岛是我国南沙群岛的一个小岛,一天某渔船在该海域捕鱼,突然发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告并立即返航,渔政船接到报告后,立即出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t的函数图象.(假设渔船和渔政船沿同一航线航行)则在渔政船驶往黄岩岛的过程中,渔船从港口出发经过9.6或10.4小时与渔政船相距30海里.
黄岩岛是我国南沙群岛的一个小岛,一天某渔船在该海域捕鱼,突然发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告并立即返航,渔政船接到报告后,立即出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t的函数图象.(假设渔船和渔政船沿同一航线航行)则在渔政船驶往黄岩岛的过程中,渔船从港口出发经过9.6或10.4小时与渔政船相距30海里.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小明在楼顶A处测得对面大楼楼顶点C处的仰角为30°,在楼底点B处的仰角为60°.若两座楼AB与CD相距60米,则楼AB的高度约为40$\sqrt{3}$米.(结果保留根号)
小明在楼顶A处测得对面大楼楼顶点C处的仰角为30°,在楼底点B处的仰角为60°.若两座楼AB与CD相距60米,则楼AB的高度约为40$\sqrt{3}$米.(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com