
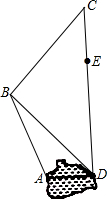
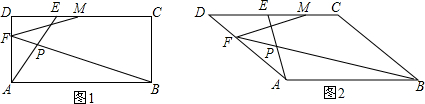
 如图是某个园区部分景点(景点A,B,C,D,E)示意图,景点A,D之间是一个荷花池,景点E,D和景点B,D之间正在维修,不能通行.已知AB=400$\sqrt{3}$米,BC=l000米,CE=600米,CD⊥AD,∠BDC=45°,∠ABD=15°.请根据以上条件求出荷花池AD的宽度和景点E,D之间的距离.
如图是某个园区部分景点(景点A,B,C,D,E)示意图,景点A,D之间是一个荷花池,景点E,D和景点B,D之间正在维修,不能通行.已知AB=400$\sqrt{3}$米,BC=l000米,CE=600米,CD⊥AD,∠BDC=45°,∠ABD=15°.请根据以上条件求出荷花池AD的宽度和景点E,D之间的距离. 分析 过B作BF⊥AD交DA的延长线于点F,过B作BG⊥CD于G,则四边形BFDG为矩形,在Rt△BFA中可求出BF,AF的长,进而可求出AD的长,在Rt△BGC中,利用勾股定理可求出CG=800米,所以CD=CG+GD=1400米,进而可求出ED=CD-CE=1400-600=800米.
解答 解:过B作BF⊥AD交DA的延长线于点F,
∵CD⊥AD,
∴BF∥DC.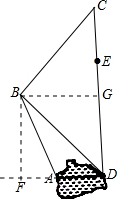
∵∠BDC=45°,
∴∠FBD=45°.
又∵∠ABD=15°,
∴∠FBA=30°.
∴在Rt△BFA中,BF=AB•cos∠FBA=400$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=600米.AF=AB•sin∠FBA=400$\sqrt{3}$×$\frac{1}{2}$=200$\sqrt{3}$米.
在Rt△BFD中,DF=BF=600米,
∴AD=DF-AF=(600-200$\sqrt{3}$)米.
过B作BG⊥CD于G,则四边形BFDG为矩形,又BF=DF,
∴四边形BFDG为正方形,
∴BG=FB=600.在Rt△BGC中,CG=$\sqrt{B{C}^{2}-B{G}^{2}}$=800米,
∴CD=CG+GD=1400米,ED=CD-CE=1400-600=800米.
∴荷花池AD宽(600-200$\sqrt{3}$)米,景点E,D之间的距离为800米.
点评 本题考查了勾股定理在直角三角形中的运用,特殊角的三角函数值的计算,三角函数在直角三角形中的运用,解题的关键正确作出高线构造直角三角形.


科目:初中数学 来源: 题型:解答题
 如图,B坐标为(2,0),AB⊥x轴于B,△ABO的面积为3.
如图,B坐标为(2,0),AB⊥x轴于B,△ABO的面积为3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
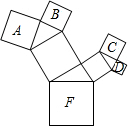 若图中正方形F以上的正方形均是以直角三角形向外作的正方形:
若图中正方形F以上的正方形均是以直角三角形向外作的正方形:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
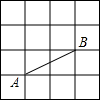 如图是正方形网格,除A,B两点外,在网格的格点上任取一点C,连接AC,BC,能使△ABC为等腰三角形的概率是( )
如图是正方形网格,除A,B两点外,在网格的格点上任取一点C,连接AC,BC,能使△ABC为等腰三角形的概率是( )| A. | $\frac{4}{23}$ | B. | $\frac{6}{23}$ | C. | $\frac{7}{23}$ | D. | $\frac{8}{23}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | 80-x | 40 |
| 销售量(件) | 200 | 200+10x | 400-10x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com