
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | 80-x | 40 |
| 销售量(件) | 200 | 200+10x | 400-10x |
分析 (1)第二个月的单价=第一个月的单价-降低的价格,销售量=200+10×降低的单价;清仓时的销售量为:800-第一个月的销售量-第二个月的销售量;
(2)等量关系为:总售价-总进价=9000.把相关数值代入计算即可.
解答 解:(1)填表:
| 时间 | 第一周 | 第二周 | 清仓时 |
| 单价(元) | 80 | 80-x | 40 |
| 销售量(件) | 200 | 200+10x | 400-10x |
点评 本题考查一元二次方程的应用;用列表格的方法得到第2个月的单价和销售量以及清仓时的销售量是解决本题的突破点;得到总利润的等量关系是解决本题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
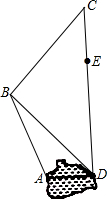 如图是某个园区部分景点(景点A,B,C,D,E)示意图,景点A,D之间是一个荷花池,景点E,D和景点B,D之间正在维修,不能通行.已知AB=400$\sqrt{3}$米,BC=l000米,CE=600米,CD⊥AD,∠BDC=45°,∠ABD=15°.请根据以上条件求出荷花池AD的宽度和景点E,D之间的距离.
如图是某个园区部分景点(景点A,B,C,D,E)示意图,景点A,D之间是一个荷花池,景点E,D和景点B,D之间正在维修,不能通行.已知AB=400$\sqrt{3}$米,BC=l000米,CE=600米,CD⊥AD,∠BDC=45°,∠ABD=15°.请根据以上条件求出荷花池AD的宽度和景点E,D之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
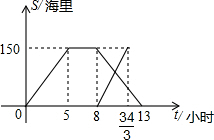 黄岩岛是我国南沙群岛的一个小岛,一天某渔船在该海域捕鱼,突然发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告并立即返航,渔政船接到报告后,立即出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t的函数图象.(假设渔船和渔政船沿同一航线航行)则在渔政船驶往黄岩岛的过程中,渔船从港口出发经过9.6或10.4小时与渔政船相距30海里.
黄岩岛是我国南沙群岛的一个小岛,一天某渔船在该海域捕鱼,突然发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告并立即返航,渔政船接到报告后,立即出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t的函数图象.(假设渔船和渔政船沿同一航线航行)则在渔政船驶往黄岩岛的过程中,渔船从港口出发经过9.6或10.4小时与渔政船相距30海里.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
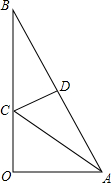 如图,直角三角形纸片OAB,∠AOB=90°,OA=1,OB=2,折叠该纸片,折痕与边OB交于点C,与边AB交于点D,折叠后点B与点A重合.
如图,直角三角形纸片OAB,∠AOB=90°,OA=1,OB=2,折叠该纸片,折痕与边OB交于点C,与边AB交于点D,折叠后点B与点A重合.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小明在楼顶A处测得对面大楼楼顶点C处的仰角为30°,在楼底点B处的仰角为60°.若两座楼AB与CD相距60米,则楼AB的高度约为40$\sqrt{3}$米.(结果保留根号)
小明在楼顶A处测得对面大楼楼顶点C处的仰角为30°,在楼底点B处的仰角为60°.若两座楼AB与CD相距60米,则楼AB的高度约为40$\sqrt{3}$米.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com