
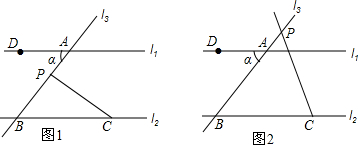
分析 (1)先根据平行线的性质得出∠α=∠PBC.再由∠APC是△PBC的一个外角得出∠APC=∠PBC+∠PCB,通过等量代换即可得出结论;
(2)由l1∥l2可知∠α=∠PBC,再根据三角形内角和定理得出∠PBC+∠PCB+∠APC=180°,利用等量代换即可得出结论.
解答 (1)证明:∵l1∥l2,
∴∠α=∠PBC.
∵∠APC是△PBC的一个外角,
∴∠APC=∠PBC+∠PCB,
∴∠APC=∠α+∠PCB.
(2)三个角的关系为:∠α+∠APC+∠PCB=180°.
证明:∵l1∥l2,
∴∠α=∠PBC.
∵∠PBC+∠PCB+∠APC=180°,
∴∠α+∠PCB+∠APC=180°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | 80-x | 40 |
| 销售量(件) | 200 | 200+10x | 400-10x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,是一个机器零件的设计图纸(单位:mm),根据图纸中的数据L=40±0.02,用不等式表示合格率零件的长度L的取值范围是( )
如图,是一个机器零件的设计图纸(单位:mm),根据图纸中的数据L=40±0.02,用不等式表示合格率零件的长度L的取值范围是( )| A. | L≤40.2 | B. | L≥39.98 | C. | 39.98≤L≤40.02 | D. | 39.8≤L≤40.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
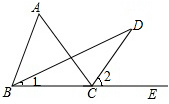 阅读下面的证明过程,在括号内补充推理的依据.
阅读下面的证明过程,在括号内补充推理的依据.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
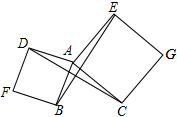 如图,以△ABC的两边AB、AC分别向外作正方形ABFD、ACGE,连接BE、DC,试猜测线段BE、DC的位置关系和数量关系,并说明理由.
如图,以△ABC的两边AB、AC分别向外作正方形ABFD、ACGE,连接BE、DC,试猜测线段BE、DC的位置关系和数量关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
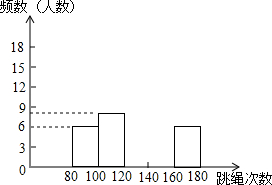 为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:
为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:| 组 别 | 次 数x | 频数(人数) |
| 第一组 | 80≤x<100 | 6 |
| 第二组 | 100≤x<120 | 8 |
| 第三组 | 120≤x<140 | a |
| 第四组 | 140≤x<160 | 18 |
| 第五组 | 160≤x<180 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
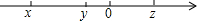 已知实数x、y、z在数轴上的对应点如图所示,化简:$\sqrt{(x-y)^{2}}$-($\sqrt{y-z}$)2+$\root{3}{(x-z)^{3}}$的值.
已知实数x、y、z在数轴上的对应点如图所示,化简:$\sqrt{(x-y)^{2}}$-($\sqrt{y-z}$)2+$\root{3}{(x-z)^{3}}$的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com