
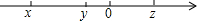 已知实数x、y、z在数轴上的对应点如图所示,化简:$\sqrt{(x-y)^{2}}$-($\sqrt{y-z}$)2+$\root{3}{(x-z)^{3}}$的值.
已知实数x、y、z在数轴上的对应点如图所示,化简:$\sqrt{(x-y)^{2}}$-($\sqrt{y-z}$)2+$\root{3}{(x-z)^{3}}$的值. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
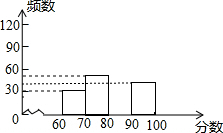 某中学组织全校1500名学生参加安全知识测试,为了解本次测试成绩的分别情况,从中随机抽取了部分学生的成绩,绘制出如图不完整的统计图表:
某中学组织全校1500名学生参加安全知识测试,为了解本次测试成绩的分别情况,从中随机抽取了部分学生的成绩,绘制出如图不完整的统计图表:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | 50 | n |
| 80≤x<90 | 80 | 0.4 |
| 90≤x<100 | 40 | 0.2 |
| 合计 | m | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com