
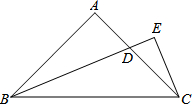
 等腰直角三角形ABC中,∠A=90°,∠B的平分线交AC于D,过点C向BD作垂线,并与BD延长线交于点E,求证:BD=2CE.
等腰直角三角形ABC中,∠A=90°,∠B的平分线交AC于D,过点C向BD作垂线,并与BD延长线交于点E,求证:BD=2CE. 分析 根据已知条件,易证△BFE≌△BCE,所以BF=BC,所以∠F=∠BCE,根据等腰三角形三线合一这一性质可得:CE=FE,再证明△ABD≌△ACF,证得BD=CF,从而证得BD=2CE.
解答 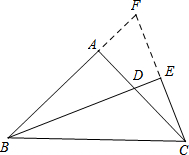 证明:延长CE,交BA延长线于点F.
证明:延长CE,交BA延长线于点F.
∵BE平分∠ABC,
∴∠ABD=∠DBC,
又∵BE⊥EC,
∴∠BEC=∠BEF=90°,
在△BEF和△BEC中,
$\left\{{\begin{array}{l}{∠ABD=∠DBC}\\{BE=BE}\\{∠BEF=∠BEC}\end{array}}\right.$,
∴△BEF≌△BEC,
∴EF=EC,
即CF=2EC,
∵AB=AC,∠BAC=90°
∴∠CAF=90°
Rt△ABD中,∠ABD+∠ADB=90°,
Rt△AEF中,∠ABD+∠F=90°,
∴∠ADB=∠F,
在△ABD和△ACF中,
$\left\{{\begin{array}{l}{∠ADB=∠F}\\{∠BAC=∠FAC}\\{AB=AC}\end{array}}\right.$,
∴△ABD≌△ACF,
∴BD=CF,
∵CF=2EC,
∴BD=2CE.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,解题的关键是熟练应用等边对等角以及等腰三角形三线合一的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
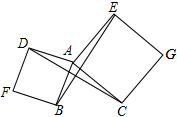 如图,以△ABC的两边AB、AC分别向外作正方形ABFD、ACGE,连接BE、DC,试猜测线段BE、DC的位置关系和数量关系,并说明理由.
如图,以△ABC的两边AB、AC分别向外作正方形ABFD、ACGE,连接BE、DC,试猜测线段BE、DC的位置关系和数量关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
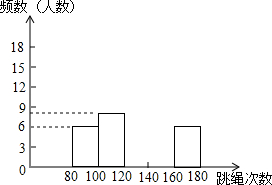 为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:
为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:| 组 别 | 次 数x | 频数(人数) |
| 第一组 | 80≤x<100 | 6 |
| 第二组 | 100≤x<120 | 8 |
| 第三组 | 120≤x<140 | a |
| 第四组 | 140≤x<160 | 18 |
| 第五组 | 160≤x<180 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
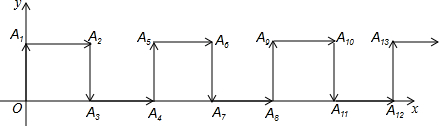
| A. | (1006,0) | B. | (1006,1) | C. | (1007,0) | D. | (1007,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
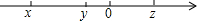 已知实数x、y、z在数轴上的对应点如图所示,化简:$\sqrt{(x-y)^{2}}$-($\sqrt{y-z}$)2+$\root{3}{(x-z)^{3}}$的值.
已知实数x、y、z在数轴上的对应点如图所示,化简:$\sqrt{(x-y)^{2}}$-($\sqrt{y-z}$)2+$\root{3}{(x-z)^{3}}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
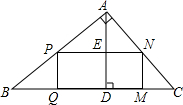 如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要使它加工成矩形零件PQMN,使矩形的一边在BC上,其他两个顶点分别在AB、AC上,并且PN=2PQ,PN的长是多少?
如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要使它加工成矩形零件PQMN,使矩形的一边在BC上,其他两个顶点分别在AB、AC上,并且PN=2PQ,PN的长是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com