
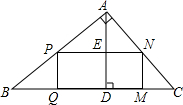
 如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要使它加工成矩形零件PQMN,使矩形的一边在BC上,其他两个顶点分别在AB、AC上,并且PN=2PQ,PN的长是多少?
如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要使它加工成矩形零件PQMN,使矩形的一边在BC上,其他两个顶点分别在AB、AC上,并且PN=2PQ,PN的长是多少? 分析 根据矩形的性质得PN∥QM,设PQ=x,则PN=2x,ED=x,AE=AD-ED=80-x,然后利用PN∥BC判断△APN∽△ABC,则根据相似三角形的性质得$\frac{80-x}{80}$=$\frac{2x}{120}$,再利用比例性质计算出x即可得到PN的长.
解答 解:∵四边形PQMN为矩形,
∴PN∥QM,
∵AD为高,
∴四边形PQDE为矩形,
∴ED=PQ,
设PQ=x,则PN=2x,ED=x,AE=AD-ED=80-x,
∵PN∥BC,
∴△APN∽△ABC,
∴$\frac{AE}{AD}$=$\frac{PN}{BC}$,即$\frac{80-x}{80}$=$\frac{2x}{120}$,
解得x=$\frac{240}{7}$,
∴PN=2x=$\frac{480}{7}$.
答:PN的长是$\frac{480}{7}$m.
点评 本题考查了相似三角形的应用:利用相似三角形的性质即相似三角形的对应边的比相等计算线段的长.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:解答题
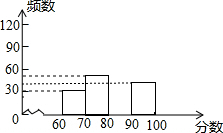 某中学组织全校1500名学生参加安全知识测试,为了解本次测试成绩的分别情况,从中随机抽取了部分学生的成绩,绘制出如图不完整的统计图表:
某中学组织全校1500名学生参加安全知识测试,为了解本次测试成绩的分别情况,从中随机抽取了部分学生的成绩,绘制出如图不完整的统计图表:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | 50 | n |
| 80≤x<90 | 80 | 0.4 |
| 90≤x<100 | 40 | 0.2 |
| 合计 | m | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ABC=90°,D为AB延长线上一点,点E在BC边上且BE=BD,连结AE、DE、DC,AE=DC.
如图,在△ABC中,∠ABC=90°,D为AB延长线上一点,点E在BC边上且BE=BD,连结AE、DE、DC,AE=DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com