
【题目】如图,抛物线y= ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() (k>0)与x轴交于点A、B,点A在点B的右边,与y轴交于点C
(k>0)与x轴交于点A、B,点A在点B的右边,与y轴交于点C
(1)如图1,若∠ACB=90°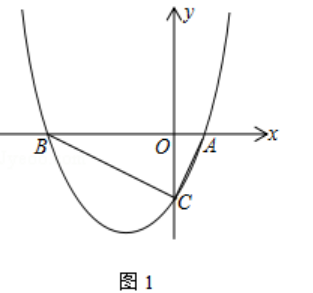
①求k的值;
②点P为x轴上方抛物线上一点,且点P到直线BC的距离为 ![]() ,则点P的坐标为(请直接写出结果)
,则点P的坐标为(请直接写出结果)
(2)如图2,当k=2时,过原点O的任一直线y=mx(m≠0)交抛物线于点E、F(点E在点F的左边)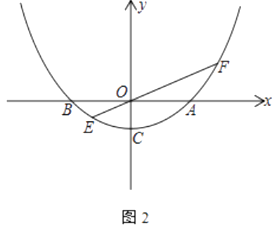
①若OF=2OE,求直线y=mx的解析式;
②求 ![]() +
+ ![]() 的值.
的值.
【答案】
(1)k=8;(﹣4﹣ ![]() ,
, ![]() )
)
(2)
解:①过点E、F分别作x轴的垂线,垂直分别为M,N.
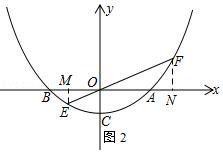
把k=2代入得:y= ![]() x2﹣1.
x2﹣1.
由 ![]() x2﹣1=mx,得到xE+xF=4m,xExF=﹣4.
x2﹣1=mx,得到xE+xF=4m,xExF=﹣4.
∵OF=2OE,
∴xF=﹣2xE,且xE<0,
∴﹣2xExE=﹣4,解得:xE=﹣ ![]() .
.
∴﹣ ![]() +2
+2 ![]() =4m,解得:m=
=4m,解得:m= ![]() .
.
∴直线的解析式为y= ![]() x.
x.
②设∠FON=α,则 ![]() +
+ ![]() =cosα(
=cosα( ![]() +
+ ![]() ).
).
∵直线EF的解析式为y=mx,
∴tanα=m,
∴cosα= ![]() .
.
∴ ![]() +
+ ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
∴ ![]() +
+ ![]() =cosα(
=cosα( ![]() +
+ ![]() )=
)= ![]()
![]() =1.
=1.
【解析】(1)①∵y= ![]() [x2+(k﹣2)x﹣2k]=
[x2+(k﹣2)x﹣2k]= ![]() (x﹣2)(x+k),
(x﹣2)(x+k),
∴点A的坐标为(2,0),点B的坐标为(﹣k,0).
∵将x=0代入抛物线的解析式为y=﹣ ![]() .
.
∴点C的坐标为(0,﹣ ![]() ).
).
∵∠BCO+∠ACO=90°,∠OBC+∠BCO=90°,
∴∠OBC=∠OCA.
又∵∠BOC=∠AOC,
∴△OBC∽△OCA.
∴ ![]() =
= ![]() .
.
∴OC2=AOOB.
∴ ![]() k2=2k,解得:
k2=2k,解得:
k=8或者k=0(舍)
②将k=8代入抛物线的解析式得:y= ![]() x2+
x2+ ![]() x﹣4.
x﹣4.
当x=0时,y=﹣4,
∴C(0,﹣4).
令y=0得: ![]() x2+
x2+ ![]() x﹣4=0,解得x=﹣8或x=2.
x﹣4=0,解得x=﹣8或x=2.
∴A(2,0)B(﹣8,0).
∴AC= ![]() =2
=2 ![]() .
.
设直线BC的解析式为y=kx+b,将点B和点C的坐标代入得: ![]() ,
,
解得: 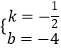 ,
,
∴直线BC的解析式为y= ![]() x﹣4.
x﹣4.
设M为AC的中点,则M(1,﹣2),如图1所示:过点M作PM∥BC,交抛物线与点P.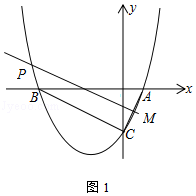
设直线PM的解析式为y=﹣ ![]() x+c,将点M的坐标代入得:﹣
x+c,将点M的坐标代入得:﹣ ![]() +c=﹣2,解得:c=﹣
+c=﹣2,解得:c=﹣ ![]() .
.
∴直线PM的解析式为y=﹣ ![]() x﹣
x﹣ ![]() .
.
∴﹣ ![]() x﹣
x﹣ ![]() =
= ![]() x2+
x2+ ![]() x﹣4,解得x=﹣4﹣
x﹣4,解得x=﹣4﹣ ![]() 或x=﹣4+
或x=﹣4+ ![]() (舍去).
(舍去).
当x=﹣4﹣ ![]() 时,y=
时,y= ![]() .
.
∴点P的坐标为(﹣4﹣ ![]() ,
, ![]() ).
).
所以答案是:(﹣4﹣ ![]() ,
, ![]() ).
).
【考点精析】解答此题的关键在于理解根与系数的关系的相关知识,掌握一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商,以及对确定一次函数的表达式的理解,了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.


科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC绕点A按顺时针方向旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若DE=2,∠B=60°,则CD的长为( ) 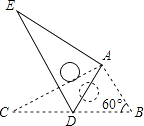
A.0.5
B.1.5
C.![]()
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(1)![]() (2)
(2)![]()
(3)![]() (4)(3x+y)(-y+3x)
(4)(3x+y)(-y+3x)
(5)2a(a-2a3)-(-3a2)2; (6)(x-3)(x+2)-(x+1)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元
(1)A商品的单价是元,B商品的单价是元
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,设购买A商品的件数为x件,该商店购买的A、B两种商品的总费用为y元 ①求y与x的函数关系式
②如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,求购买B商品最多有多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线 l 上依次摆放着七个正方形(如图所示),已知斜放置的三个正方形的面积分别 为 a,b,c,正放置的四个正方形的面积依次为 S1,S2,S3,S4,则 S1+S2+S3+S4=( )
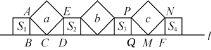
A. a+b B. b+c C. a+c D. a+b+c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
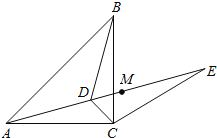
(1)求证:DE平分∠BDC;
(2)若点M在DE上,且DC=DM,求证:ME=BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1 , A3B3C3C2 , …按如图的方式放置.点A1 , A2 , A3 , …和点C1 , C2 , C3 , …分别在直线y=x+1和x轴上,则点B6的坐标是 . 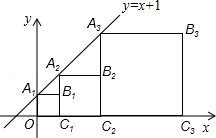
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=4,BC=6.将该矩形纸片剪去3个等腰直角三角形,所有剪法中剩余部分面积的最小值是( )
A.6
B.3
C.2.5
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com