
【题目】计算:(1)![]() (2)
(2)![]()
(3)![]() (4)(3x+y)(-y+3x)
(4)(3x+y)(-y+3x)
(5)2a(a-2a3)-(-3a2)2; (6)(x-3)(x+2)-(x+1)2
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() ;(5)
;(5)![]() ;(6)
;(6)![]() .
.
【解析】
(1)先进行乘方运算,然后再利用单项式的乘除法法则按顺序进行计算即可;
(2)先利用完全平方公式进行展开,然后再合并同类项即可;
(3)利用单项式乘多项式的法则进行计算即可;
(4)利用平方差公式进行计算即可;
(5)先进行单项式乘多项式运算、积的乘方运算,然后再合并同类项即可;
(6)利用多项式乘多项式法则以及完全平方公式进行展开,然后再合并同类项即可.
(1)原式=![]()
![]()
![]() =-18×
=-18×![]() ×6xy5z3=
×6xy5z3=![]() ;
;
(2)原式=![]() =
=![]() ;
;
(3)原式=![]() ;
;
(4)(3x+y)(-y+3x)=(3x)2-y2=9x2-y2;
(5)原式=2a2-4a4-9a4=2a2-13a4;
(6)原式=x2-x-6-(x2+2x+1)=-3x-7.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论: ①b2>4ac;
②abc>0;
③2a﹣b=0;
④8a+c<0;
⑤9a+3b+c<0.
其中结论正确的是 . (填正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E为CD上一点,F为BC延长线上一点,CE=CF. 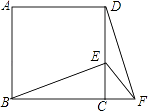
(1)△DCF可以看做是△BCE绕点C旋转某个角度得到的吗?说明理由.
(2)若∠CEB=60°,求∠EFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AB是⊙O的直径,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°. 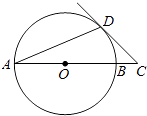
(1)求证:CD是⊙O的切线;
(2)若AB=2 ![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为a的正方形中挖掉一个边长为b的小正方形(a>b).把余下的部分剪拼成一个矩形(如图).通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
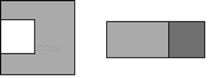
A. a2﹣b2=(a+b)(a﹣b) B. (a+b)2=a2+2ab+b2
C. (a﹣b)2=a2﹣2ab+b2 D. a2﹣ab=a(a﹣b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义函数f(x),当x≤3时,f(x)=x2﹣2x,当x>3时,f(x)=x2﹣10x+24,若方程f(x)=2x+m有且只有两个实数解,则m的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() (k>0)与x轴交于点A、B,点A在点B的右边,与y轴交于点C
(k>0)与x轴交于点A、B,点A在点B的右边,与y轴交于点C
(1)如图1,若∠ACB=90°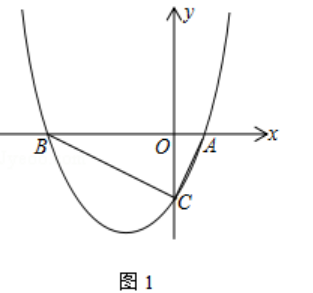
①求k的值;
②点P为x轴上方抛物线上一点,且点P到直线BC的距离为 ![]() ,则点P的坐标为(请直接写出结果)
,则点P的坐标为(请直接写出结果)
(2)如图2,当k=2时,过原点O的任一直线y=mx(m≠0)交抛物线于点E、F(点E在点F的左边)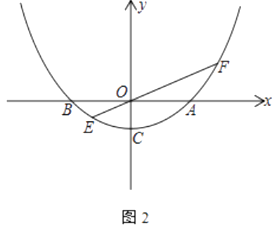
①若OF=2OE,求直线y=mx的解析式;
②求 ![]() +
+ ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将半径为3cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
普通消费:35元/次;
白金卡消费:购卡280元/张,凭卡免费消费10次再送2次;
钻石卡消费:购卡560元/张,凭卡每次消费不再收费.
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用.
(1)李叔叔每年去该健身中心健身6次,他应选择哪种消费方式更合算?
(2)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
(3)王阿姨每年去该健身中心健身至少18次,请通过计算帮助王阿姨选择最合算的消费方式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com