
【题目】如图,已知直线y=ax+b与双曲线y=(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
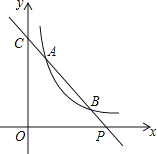
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).
【答案】(1)P(4,O);(2)A(2,2),B(4,1).(3)x1+x2=x0.
【解析】
试题分析:(1)先把A(1,3)),B(3,y2)代入y=![]() 求得反比例函数的解析式,进而求得B的坐标,然后把A、B代入y=ax+b利用待定系数法即可求得直线的解析式,继而即可求得P的坐标;
求得反比例函数的解析式,进而求得B的坐标,然后把A、B代入y=ax+b利用待定系数法即可求得直线的解析式,继而即可求得P的坐标;
(2)作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,则AD∥BG∥x轴,AE∥BF∥y轴,得出![]() ,
,![]() ,根据题意得出
,根据题意得出![]() ,
,![]() ,从而求得B(
,从而求得B(![]() ,
,![]() y1),然后根据k=xy得出x1
y1),然后根据k=xy得出x1 ![]() y1=
y1=![]()
![]() y1,求得x1=2,代入
y1,求得x1=2,代入![]() ,解得y1=2,即可求得A、B的坐标;
,解得y1=2,即可求得A、B的坐标;
(3)结合(1),(2)中的结果,猜想x1+x2=x0.
试题解析:(1)∵直线y=ax+b与双曲线y=![]() (x>0)交于A(1,3),
(x>0)交于A(1,3),
∴k=1×3=3,
∴y=![]() ,
,
∵B(3,y2)在反比例函数的图象上,
∴y2=![]() =1,
=1,
∴B(3,1),
∵直线y=ax+b经过A、B两点,
∴![]() 解得
解得![]() ,
,
∴直线为y=-x+4,
令y=0,则x=4,
∴P(4,O);
(2)如图,作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,
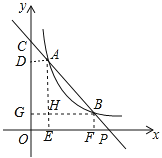
则AD∥BG∥x轴,AE∥BF∥y轴,
∴![]() ,
,![]() ,
,
∵b=y1+1,AB=BP,
∴![]() ,
,![]() ,
,
∴B(![]() ,
,![]() y1)
y1)
∵A,B两点都是反比例函数图象上的点,
∴x1y1=![]()
![]()
![]() y1,
y1,
解得x1=2,
代入![]() ,解得y1=2,
,解得y1=2,
∴A(2,2),B(4,1).
(3)根据(1),(2)中的结果,猜想:x1,x2,x0之间的关系为x1+x2=x0.


科目:初中数学 来源: 题型:
【题目】袋子中装有2个黑球和3个白球,这些球除了颜色不同外形状、大小、质地等完全相同,在看不到球的条件下,随机地一次从袋子中摸出三个球.下列事件是必然事件的是( )
A.摸出的三个球中至少有一个球是白球
B.摸出的三个球中至少有一个球是黑球
C.摸出是三个球中至少有两个球的黑球
D.摸出的单个球中至少有两个球是白球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,点D是△ABC外的一点,点E在BC边的延长线上,BD平分∠ABC,CD平分∠ACE.试探究∠D与∠A的数量关系.
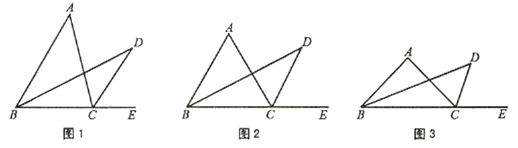
(1)特例探究:
如图2,若△ABC是等边三角形,其余条件不变,则∠D=;
如图3,若△ABC是等腰三角形,顶角∠A=100°,其余条件不变,则∠D=;这两个图中,与∠A度数的比是 ;
(2)猜想证明:
如图1,△ABC为一般三角形,在(1)中获得的∠D与∠A的关系是否还成立?若成立,利用图1证明你的结论;若不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,某团体组织公益活动,16名成员分甲、乙、丙三组到48个单位做宣传,若甲组a人每人负责4个单位,乙组b人每人负责3个单位,丙组每人负责1个单位,则分组方案有( )
A.5种 B.6种 C.7种 D.8种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com