

分析 (1)先判断出EF∥AB,进而得出△CEF是等边三角形,即可得出结论;
(2)①由对称得出∠EDF=∠ECF=60°,EC=ED,FC=FD,进而得出∠BDF=∠DEA即可得出结论;
②先表示出ED,DF,EA,DB,AD,BF,进而借助①的结论即可得出,$\frac{a}{b}=\frac{3x-a}{2x}=\frac{x}{3x-b}$,处理即可得出结论;
(3)同(2)②的方法即可得出结论.
解答 解:(1)∵D是AB的中点,△ABC是等边三角形,
∴CD⊥AB,
∵EF⊥CD,
∴EF∥AB,
∴△CEF是等边三角形,
∴CE=CF,
∴CE:CF=1:1;
(2)①∵△EFC与△EFD关于EF对称,
∴∠EDF=∠ECF=60°,EC=ED,FC=FD,
∵∠BDF+∠EDF=∠BDE=∠A+∠DEA,
∵∠EDF=∠A=60°,
∴∠BDF=∠DEA,
∴△ADE∽△BFD,
②设AD=x,CE=DE=a,CF=DF=b,
∵AD:BD=1:2,
∴DB=2x,
∴AB=3x=AC=BC,
∴AE=3x-a,BF=3x-b,
由①知,△ADE∽△BFD,
∴$\frac{ED}{DF}=\frac{EA}{DB}=\frac{AD}{BF}$,
∴$\frac{a}{b}=\frac{3x-a}{2x}=\frac{x}{3x-b}$,
由前两项得,2ax=b(3x-a),
由后两项得,(3x-a)(3x-b)=2x2,
即:3x(3x-a)-b(3x-a)=2x2,
∴3x(3x-a)-2ax=2x2,
∴a=$\frac{7}{5}$x,
∴$\frac{a}{b}=\frac{3x-a}{2x}=\frac{4}{5}$,
∴CE:CF=4:5;
(3)设AD=x,CE=DE=a,CF=DF=b,
∵AD:DB=1:n,
∴AB=(n+1)x=AC=BC,
∴AE=(n+1)x-a,BF=(n+1)x-b,
同①的方法得,△ADE∽△BFD,
∴$\frac{ED}{DF}=\frac{EA}{DB}=\frac{AD}{BF}$,
∴$\frac{a}{b}=\frac{(n+1)x-a}{nx}=\frac{x}{(n+1)x-b}$,
由前两项得,nax=b[(n+1)x-a],
由后两项得,[(n+1)x-a][(n+1)x-b]=nx2,
∴(n+1)[(n+1)x-a]-b[(n+a)-b]=nx2,
∴(n+1)[(n+1)x-a]-nax=nx2,
解得,a=$\frac{{n}^{2}+n+1}{2n+1}$x,
∴$\frac{a}{b}=\frac{(n+1)x-a}{nx}=\frac{n+2}{2n+1}$,
∴CE:CF=(n+2):(2n+1).
点评 此题是相似形综合题,主要考查了等边三角形的性质,对称的性质,相似三角形的判定和性质,解(1)的关键是得出EF∥AB,解(2)的关键是得出∠BDF=∠DEA,难点是对$\frac{a}{b}=\frac{3x-a}{2x}=\frac{x}{3x-b}$的处理,解(3)的关键是对$\frac{a}{b}=\frac{(n+1)x-a}{nx}=\frac{x}{(n+1)x-b}$的处理,是一道计算量比较大的题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
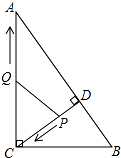 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D,点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D,点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
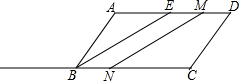 如图,在平行四边形ABCD中,AD=2AB=6cm,BE是∠ABC的角平分线,点M从点E出发,沿ED方向以1cm/s的速度向点D运动,点N从点C出发,沿射线CB方向运动,以4cm/s的运动速度,当点M运动到点D时,点N随之停止运动,设运动时间为t秒.
如图,在平行四边形ABCD中,AD=2AB=6cm,BE是∠ABC的角平分线,点M从点E出发,沿ED方向以1cm/s的速度向点D运动,点N从点C出发,沿射线CB方向运动,以4cm/s的运动速度,当点M运动到点D时,点N随之停止运动,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com