Question

11．如图，在平面直角坐标系xOy中，已知等腰直角△APB，∠PAB=90°且点A（4，2），过点A作x轴的垂线交直线y=-$\frac{1}{4}$x于点N，动点P在线段ON上，点B随点P的运动而运动；
（1）当点P与点N重合时，求点B的坐标．
（2）若点P的横坐标为3，求直线BP的解析式．
（3）连接BN，若BN=BA，求△ABN的面积．

Answer 1

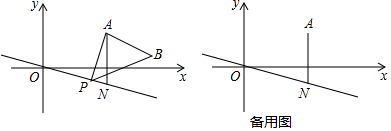
分析 先求出点N的坐标，进而求出AN=3．
（1）先判断出AB∥x轴，再求出AB=AN=3，即可得出点B的坐标；
（2）先确定出点P的坐标，再求出PF，AF，另为判断出△AFP≌△BEA，得出AE=PF=1，BE=AF=$\frac{11}{4}$，即可确定出点B的坐标，最后用待定系数法求出直线BP的解析式；
（3）先求出AE，再借助（2）的结论得出PF即可求出点P的坐标，进而求出BE，最后用三角形的面积即可得出结论．

解答 解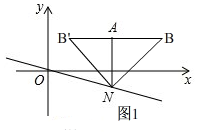：∵点A（4，2），过点A作x轴的垂线交直线y=-$\frac{1}{4}$x于点N，
∴N（4，-1），
∴AN=3，
（1）如图1，当点P和点N重合何时，AP=AN=3，
∵∠PAB=90°，
∴AB∥x轴，
∵等腰直角△APB，
∴AB=AP=3，
∴B（7，2）或（1，2）；
（2）如图2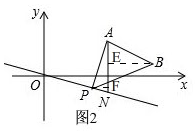，∵点P在线段ON上，且P的横坐标为3，
∴纵坐标为-$\frac{1}{4}$×3=-$\frac{3}{4}$，
∴P（3，-$\frac{3}{4}$），
∵A（4，2），过点P作PF⊥AN于F，过B作BE⊥AN于E，
∴PF=1，AF=2-（-$\frac{3}{4}$）=$\frac{11}{4}$，
∵BE⊥AN，
∴∠BAE+∠ABE=90°，
∵∠PAF+∠BPF=90°，
∴∠PAF=∠ABE，
在△AFP和△BEA中，$\left\{\begin{array}{l}{∠AFP=∠BEA}\\{∠PAF=∠ABE}\\{AP=AB}\end{array}\right.$，
∴△AFP≌△BEA，
∴AE=PF=1，BE=AF=$\frac{11}{4}$，
∴B的横坐标为4+$\frac{11}{4}$=$\frac{27}{4}$，B的纵坐标为2-1=1，
∴B（$\frac{27}{4}$，1），
∵P（3，-$\frac{3}{4}$），
∴直线BP的解析式为y=$\frac{7}{15}$x-$\frac{43}{20}$；
（3）如图3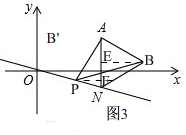，过点B作BE⊥AN于E，
∵BN=AB，
∴AE=$\frac{1}{2}$AN=$\frac{3}{2}$，
由（2）知，PF=AE=$\frac{3}{2}$，
∴P点的横坐标为4-$\frac{3}{2}$=$\frac{5}{2}$，
∴P的纵坐标为-$\frac{1}{4}$×$\frac{5}{2}$=-$\frac{5}{8}$，
∴AF=2-（-$\frac{5}{8}$）=$\frac{21}{8}$
∴BE=AF=$\frac{21}{8}$，
∴S_△ABN=$\frac{1}{2}$AN•BE=$\frac{1}{2}$×3×$\frac{21}{8}$=$\frac{63}{16}$．

点评 此题是一次函数综合题，主要考查了待定系数法，等腰直角三角形的性质，全等三角形的判定和性质，三角形的面积公式；解（1）的关键是得出AB平行于x轴，解（2）的关键是判断出△AFP≌△BEA，解（3）的关键是求出点P的坐标，是一道中等难度的中考常考题．