

分析 (1)如图(1),作两弦的弦心距OG和OH,由垂径定理得:AG=$\frac{1}{2}$AB,AH=$\frac{1}{2}$AC,所以AG=AH,再证明Rt△AGO≌Rt△AHO可得结论;
(2)如图(2),作辅助线,构建三角形全等,证明△ABF≌△ACD(AAS),得BF=CN,AF=AN,再根据HL证明Rt△AFD≌Rt△AND,根据对应边相等DF=DN,可得结论;
(3)如图3中,连接AD、OH.只要证明△AOF,△DOH都是等腰直角三角形,∠E=∠HDE=22.5°即可解决问题.
解答 证明:(1)如图(1),过O作OG⊥AB于G,OH⊥AC于H,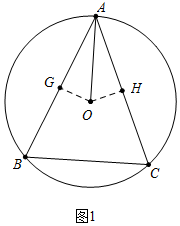
∴AG=$\frac{1}{2}$AB,AH=$\frac{1}{2}$AC,
∵∠ACB=∠ABC,
∴AB=AC,
∴AG=AH,
∵AO=AO,
∴Rt△AGO≌Rt△AHO(HL),
∴∠BAO=∠CAO,
∴AO平分∠BAC;
(2)如图(2),过A作AN⊥CD,交CD的延长线于N,连接AD,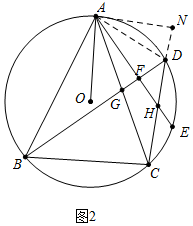
∵AF⊥BD,
∴∠AFB=∠ANC=90°,
∵AB=AC,∠ABD=∠ACD,
∴△ABF≌△ACD(AAS),
∴BF=CN,AF=AN,
∵AD=AD,
∴Rt△AFD≌Rt△AND(HL),
∴DF=DN,
∴BD+CD=BF+DF+CD=BF+DN+CD=BF+CN=BF+BF=2BF;
(3)如图3中,连接AD、OH.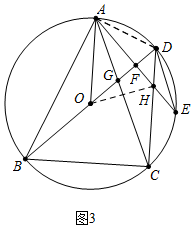
∵OA∥CD,
∴∠AOG=∠ODH,
在△AOG和△ODH中,
$\left\{\begin{array}{l}{OA=OD}\\{∠AOG=∠ODH}\\{OG=DH}\end{array}\right.$,
∴△AOG≌△ODH,
∴∠OAG=∠DOH=∠DAH,
∵∠AFD=∠OFH,
∴△AFD∽△OFH,
∴$\frac{AF}{OF}$=$\frac{DF}{FH}$,
∴$\frac{AF}{DF}$=$\frac{OF}{FH}$,
∴△AFO∽△DFH,
∴∠OAF=∠FDH,
∵∠AOF=∠FDH,
∴∠FAO=∠FOA=45°,∠FDH=∠FHD=45°,
∴AF=OF=FE,DF=DH,
∴∠OAG=∠HAD,∠AOG=∠AHD,OG=DH,
∴△AOG≌△AHD,
∴AG=AD,∵AF⊥DG,
∴∠GAF=∠FAD=∠OAG=22.5°,
∴∠AED=∠HDE=22.5°,设DF=FH=a,则DH=HE=$\sqrt{2}$a,
∵$\frac{1}{2}$•HE•DF=9$\sqrt{2}$,
∴$\frac{1}{2}$$•\sqrt{2}$a•a=9$\sqrt{2}$,
∴a=3$\sqrt{2}$,
∴AF=EF=OF=6+3$\sqrt{2}$,
∴⊙O的半径OD=6+6$\sqrt{2}$.
点评 本题考查圆综合题、全等三角形的判定和性质.相似三角形的判定和性质、角平分线的判定和性质等腰直角三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题,第三个问题的突破点是证明△AOF,△DOH都是等腰直角三角形,∠E=∠HDE=22.5°,属于中考压轴题.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:解答题
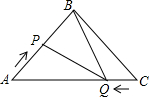 如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.
如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
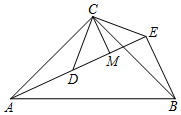 如图,已知△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM⊥AE于点M,连结BE.
如图,已知△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM⊥AE于点M,连结BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
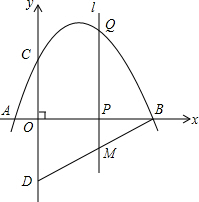 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{5}{2}$x+3 与 x 轴交于点 A,点 B,与 y 轴交于点C,点D 与点C关于 x 轴对称,点 P 是 x 轴上的一个动点,设点P 的坐标为(m,0),过点 P 作 x 轴的垂线 l 交抛物线于点 Q.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{5}{2}$x+3 与 x 轴交于点 A,点 B,与 y 轴交于点C,点D 与点C关于 x 轴对称,点 P 是 x 轴上的一个动点,设点P 的坐标为(m,0),过点 P 作 x 轴的垂线 l 交抛物线于点 Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com