练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知关于x的方程kx2+（1﹣k）x﹣1=0，下列说法正确的是（ ）
    A.当k=0时，方程无解
    B.当k=1时，方程有一个实数解
    C.当k=﹣1时，方程有两个相等的实数解
    D.当k≠0时，方程总有两个不相等的实数解

    【答案】C
    【解析】解：关于x的方程kx2+（1﹣k）x﹣1=0， A、当k=0时，x﹣1=0，则x=1，故此选项错误；
    B、当k=1时，x2﹣1=0方程有两个实数解，故此选项错误；
    C、当k=﹣1时，﹣x2+2x﹣1=0，则（x﹣1）2=0，此时方程有两个相等的实数解，故此选项正确；
    D、由C得此选项错误．
    故选：C．
    利用k的值，分别代入求出方程的根的情况即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】向东走5m，记为+5m，那么走﹣10m，表示（　　）

    A. 向西走10m B. 向东走10m C. 向南走10m D. 向北走10m

    查看答案和解析>>

    科目：初中数学 来源： 题型：

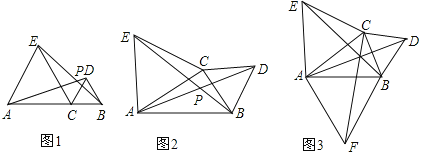
    【题目】在数学探究课上，老师出示了这样的探究问题，请你一起来探究：已知：C是线段AB所在平面内任意一点，分别以AC、BC为边，在AB同侧作等边△ACE和△BCD，连结AD、BE交于点P．

    （1）如图1，当点C在线段AB上移动时，线段AD 与BE的数量关系： ．

    （2）如图2，当点C在直线AB外，且∠ACB＜120°，上面的结论是否还成立？若成立请证明，不成立说明理由．

    （3）如图3，在（2）的条件下，以AB为边在AB另一侧作等边三角形△ABF，连结AD、BE和CF交于点P，求证：PB+PC+PA=BE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先化简再求值：

    ﹣(3a2﹣4ab)+[a2﹣2(2a+2ab)]，其中a=﹣2，b=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校学生利用双休时间去距学校10km的炎帝故里参观，一部分学生骑自行车先走，过了20min后，其余学生乘汽车沿相同路线出发，结果他们同时到达.已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度和汽车的速度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

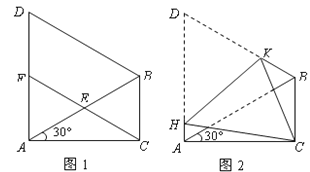
    【题目】如图1,在△ABC中，∠ACB=90°，∠CAB=30°, △ABD是等边三角形，E是AB的中点，连结CE并延长交AD于F，如图2，现将四边形ACBD折叠,使D与C重合，HK为折痕，则sin∠ACH的值为（ ）

    A． B． C． D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随机从甲、乙两块试验田中各抽取100株麦苗测量高度，甲、乙两块试验田的平均数都是13，方差结果为：S甲2=36，S乙2=158，则小麦长势比较整齐的试验田是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一元二次方程x2+x-2=0根的情况是___________________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

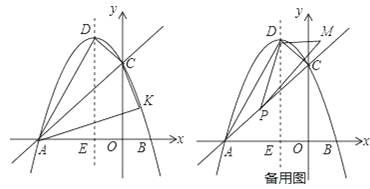
    【题目】平面直角坐标系中，抛物线y=ax2+bx+c交x轴于A，B两点（点A在点B左侧），与y轴交于点C，点A，C的坐标分别为（-3，0），（0，3），对称轴直线x=-1交x轴于点E，点D为顶点．

    （1）求抛物线的解析式；

    （2）点K是直线AC下方的抛物线上一点，且S△KAC=S△DAC求点K的坐标；

    （3）如图2若点P是线段AC上的一个动点，∠DPM=30°，DP⊥DM，则点P的线段AC上运动时，D点不变，M点随之运动，求当点P从点A运动到点C时，点M运动的路径长．

    查看答案和解析>>

    同步练习册答案