
ЎҫМвДҝЎҝЖҪГжЦұҪЗЧшұкПөЦРЈ¬ЕЧОпПЯy=ax2+bx+cҪ»xЦбУЪAЈ¬BБҪөгЈЁөгAФЪөгBЧуІаЈ©Ј¬УлyЦбҪ»УЪөгCЈ¬өгAЈ¬CөДЧшұк·ЦұрОӘЈЁ-3Ј¬0Ј©Ј¬ЈЁ0Ј¬3Ј©Ј¬¶ФіЖЦбЦұПЯx=-1Ҫ»xЦбУЪөгEЈ¬өгDОӘ¶ҘөгЈ®
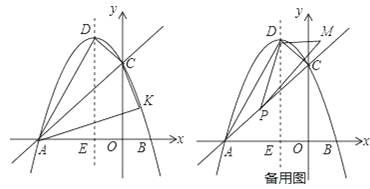
ЈЁ1Ј©ЗуЕЧОпПЯөДҪвОцКҪЈ»
ЈЁ2Ј©өгKКЗЦұПЯACПВ·ҪөДЕЧОпПЯЙПТ»өгЈ¬ЗТSЎчKAC=SЎчDACЗуөгKөДЧшұкЈ»
ЈЁ3Ј©ИзНј2ИфөгPКЗПЯ¶ОACЙПөДТ»ёц¶ҜөгЈ¬ЎПDPM=30ЎгЈ¬DPЎНDMЈ¬ФтөгPөДПЯ¶ОACЙПФЛ¶ҜКұЈ¬DөгІ»ұдЈ¬MөгЛжЦ®ФЛ¶ҜЈ¬ЗуөұөгPҙУөгAФЛ¶ҜөҪөгCКұЈ¬өгMФЛ¶ҜөДВ·ҫ¶іӨЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©y=-x2-2x+3Ј»ЈЁ2Ј©өгKөДЧшұкОӘЈЁ![]() Ј¬
Ј¬![]() Ј©»тЈЁ
Ј©»тЈЁ![]() Ј¬
Ј¬![]() Ј©Ј»(3)
Ј©Ј»(3) ![]() Ј®
Ј®
ЎҫҪвОцЎҝ
КФМв·ЦОцЈәЈЁ1Ј©ёщҫЭМхјюҝЙөГөҪ№ШУЪaЎўbЎўcөДИэФӘТ»ҙО·ҪіМЧйЈ¬Ц»РиҪвХвёц·ҪіМЧйҫНҝЙҪвҫцОКМвЈ»
ЈЁ2Ј©№эөгDЧчDHЎНyЦбУЪHЈ¬Б¬ҪУEKҪ»yЦбУЪFЈ¬Б¬ҪУECЈ¬ИзНј1Ј¬ФЛУГёоІ№·ЁҝЙЗуіцЎчDACөДГж»эЈ¬ТЧөГSЎчADC=SЎчAECЈ¬УЙSЎчKAC=SЎчDACЈ¬ҝЙөГSЎчKAC=SЎчEACЈ¬ҙУ¶шҝЙөГEKЎОACЈ¬ёщҫЭЖҪРРПЯ·ЦПЯ¶ОіЙұИАэҝЙЗуіцOFЈ¬И»әуФЛУГҙэ¶ЁПөКэ·ЁҝЙЗуіцЦұПЯEKөДҪвОцКҪЈ¬Ц»РиЗуіцЦұПЯEKУлЕЧОпПЯөДҪ»өгЧшұкҫНҝЙҪвҫцОКМвЈ»
ЈЁ3Ј©ЙиөгPФЪөгAҙҰКұөгMФЪөгMЎдЈ¬өгPФЪөгCҙҰКұөгMФЪөгMЎеЈ¬ИзНј2Ј®ТЧЦӨЎчDPCЎЧЎчDMMЎеЈ¬ЎчDACЎЧЎчDMЎдMЎеЈ¬ҙУ¶шҝЙөГЎПDMЎеM=ЎПDMЎеMЎд=ЎПDCPЈ¬УЙУЪЎПDCPКЗ¶ЁЦөЈ¬ТтҙЛөгMөДФЛ¶ҜВ·ҫ¶КЗПЯ¶ОMЎдMЎеЈ¬И»әуЦ»РиёщҫЭЎчDMЎдMЎеЎЧЎчDACЈ¬ФЛУГПаЛЖИэҪЗРОөДРФЦКҫНҝЙҪвҫцОКМвЈ®
КФМвҪвОцЈәЈЁ1Ј©УЙМвТвҝЙөГЈ¬
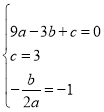 ҪвөГ
ҪвөГ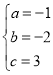 Ј¬
Ј¬
ЎаЕЧОпПЯөДҪвОцКҪОӘy=-x2-2x+3Ј»
ЈЁ2Ј©№эөгDЧчDHЎНyЦбУЪHЈ¬Б¬ҪУEKҪ»yЦбУЪFЈ¬Б¬ҪУECЈ¬ИзНј1Ј®

УЙy=-x2-2x+3=-ЈЁx+1Ј©2+4ҝЙөГ¶ҘөгDОӘЈЁ-1Ј¬4Ј©Ј¬
ЎаSЎчADC=SМЭРОAOHD-SЎчOAC-SЎчDHC
=![]() ЈЁ1+3Ј©ЎБ4-
ЈЁ1+3Ј©ЎБ4-![]() ЎБ3ЎБ3-
ЎБ3ЎБ3-![]() ЎБ1ЎБЈЁ4-3Ј©=3Ј®
ЎБ1ЎБЈЁ4-3Ј©=3Ј®
УЦЎЯSЎчAEC=![]() AE
AE![]() OC=
OC=![]() ЎБ2ЎБ3=3Ј¬
ЎБ2ЎБ3=3Ј¬
ЎаSЎчADC=SЎчAECЈ®
ЎЯSЎчKAC=SЎчDACЈ¬
ЎаSЎчKAC=SЎчEACЈ¬
ЎаEKЎОACЈ¬
Ўа![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ЎаOF=1Ј¬FЈЁ0Ј¬1Ј©Ј®
ЙиЦұПЯEKөДҪвОцКҪОӘy=mx+nЈ¬ФтУР![]() Ј¬
Ј¬
ҪвөГ![]() Ј¬
Ј¬
ЎаЦұПЯEKөДҪвОцКҪОӘy=x+1Ј®
Ҫв·ҪіМЧй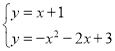 Ј¬өГ
Ј¬өГ Ј¬
Ј¬
ЎаөгKөДЧшұкОӘЈЁ![]() Ј¬
Ј¬![]() Ј©»тЈЁ
Ј©»тЈЁ![]() Ј¬
Ј¬![]() Ј©Ј»
Ј©Ј»
ЈЁ3Ј©ЙиөгPФЪөгAҙҰКұөгMФЪөгMЎдЈ¬өгPФЪөгCҙҰКұөгMФЪөгMЎеЈ¬ИзНј2Ј®

ЎЯЎПCDMЎе=ЎПPDM=90ЎгЈ¬ЎПDPM=ЎПDCMЎе=30ЎгЈ¬
Ўа![]() Ј¬ЎПPDC=ЎПMDMЎеЈ¬
Ј¬ЎПPDC=ЎПMDMЎеЈ¬
ЎаЎчDPCЎЧЎчDMMЎеЈ¬
ЎаЎПDCP=ЎПDMЎеMЈ®
Н¬АнҝЙөГЎчDACЎЧЎчDMЎдMЎеЈ¬
ЎаЎПDCA=ЎПDMЎеMЎдЈ®
ЎаЎПDMЎеM=ЎПDMЎеMЎд=ЎПDCPЈ¬
ЎЯЎПDCPКЗ¶ЁЦөЈ¬
ЎаөгMөДФЛ¶ҜВ·ҫ¶КЗПЯ¶ОMЎдMЎеЈ®
ЎЯЎчDMЎдMЎеЎЧЎчDACЈ¬
Ўа![]() Ј®
Ј®
ЎЯAC=![]() Ј¬
Ј¬
ЎаMЎдMЎе=![]() Ј¬
Ј¬
ЎаөгMөДФЛ¶ҜВ·ҫ¶іӨОӘ![]() Ј®
Ј®


 ХгҙуУЕѧСѧДкј¶ПОҪУҪЭҫ¶ХгҪӯҙуС§іц°жЙзПөБРҙр°ё
ХгҙуУЕѧСѧДкј¶ПОҪУҪЭҫ¶ХгҪӯҙуС§іц°жЙзПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘ№ШУЪxөД·ҪіМkx2+ЈЁ1©ҒkЈ©x©Ғ1=0Ј¬ПВБРЛө·ЁХэИ·өДКЗЈЁ Ј©
A.өұk=0КұЈ¬·ҪіМОЮҪв
B.өұk=1КұЈ¬·ҪіМУРТ»ёцКөКэҪв
C.өұk=©Ғ1КұЈ¬·ҪіМУРБҪёцПаөИөДКөКэҪв
D.өұkЎЩ0КұЈ¬·ҪіМЧЬУРБҪёцІ»ПаөИөДКөКэҪв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ЎСEөДФІРДE(3Ј¬0)Ј¬°лҫ¶ОӘ5Ј¬ЎСEУлyЦбПаҪ»УЪAЎўBБҪөг(өгAФЪөгBөДЙП·Ҫ)Ј¬УлxЦбөДХэ°лЦбПаҪ»УЪөгCЈ»ЦұПЯlөДҪвОцКҪОӘy=![]() xЈ«4Ј¬УлxЦбПаҪ»УЪөгDЈ»ТФCОӘ¶ҘөгөДЕЧОпПЯҫӯ№эөгB.
xЈ«4Ј¬УлxЦбПаҪ»УЪөгDЈ»ТФCОӘ¶ҘөгөДЕЧОпПЯҫӯ№эөгB.
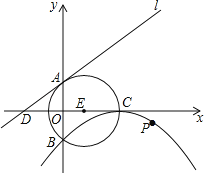
(1)ЗуЕЧОпПЯөДҪвОцКҪЈ»
(2)ЕР¶ПЦұПЯlУлЎСEөДО»ЦГ№ШПөЈ¬ІўЛөГчАнУЙЈ»
(3) ¶ҜөгPФЪЕЧОпПЯЙПЈ¬өұөгPөҪЦұПЯlөДҫаАлЧоРЎКұЈ¬ЗуіцөгPөДЧшұкј°ЧоРЎҫаАл.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДЬЦӨГчГьМвxКЗКөКэЈ¬ФтЎ°ЈЁx©Ғ3Ј©2Јҫ0ЎұКЗјЩГьМвөД·ҙАэКЗЈЁ Ј©
A.x=1
B.x=2
C.x=3
D.x=4
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДі№ӨіМіР°ь·ҪЦё¶ЁУЙјЧЎўТТБҪёц№ӨіМ¶УНкіЙДіПо№ӨіМЈ¬ИфУЙјЧ№ӨіМ¶УөҘ¶АЧцРиТӘ40МмНкіЙЈ¬ПЦФЪјЧЎўТТБҪёц№ӨіМ¶У№ІН¬Чц20МмәуЈ¬УЙУЪјЧ№ӨіМ¶УБнУРЖдЛьИООсІ»ФЩЧцёГ№ӨіМЈ¬КЈПВ№ӨіМУЙТТ№ӨіМ¶УФЩөҘ¶АЧцБЛ20МмІЕНкіЙИООсЈ®
ЈЁ1Ј©ЗуТТ№ӨіМ¶УөҘ¶АНкіЙёГ№ӨіМРиТӘ¶аЙЩМмЈҝ
ЈЁ2Ј©Из№ы№ӨіМіР°ь·ҪТӘЗуТТ№ӨіМ¶УөД№ӨЧчКұјдІ»ДЬі¬№э30МмЈ¬ТӘНкіЙёГ№ӨіМЈ¬јЧ№ӨіМ¶УЦБЙЩТӘ№ӨЧч¶аЙЩМмЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝОӘБЛҪвДіКРІОјУЦРҝјөД25000ГыС§ЙъөДМеЦШЗйҝцЈ¬ійІйБЛЖдЦР1500ГыС§ЙъөДМеЦШҪшРРНіјЖ·ЦОцЈ¬ПВБРРрКцХэИ·өДКЗЈЁ Ј©
A.25000ГыС§ЙъКЗЧЬМеB.ГҝГыС§ЙъКЗЧЬМеөДТ»ёцёцМе
C.1500ГыС§ЙъөДМеЦШКЗЧЬМеөДТ»ёцСщұҫD.СщұҫИЭБҝКЗ1500Гы
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФІРД¶јФЪxЦбХэ°лЦбЙПөД°лФІO1Ўў°лФІO2ЎўЎӯЎў°лФІOnУлЦұПЯy=![]() xПаЗРЈ¬Йи°лФІO1Ўў°лФІO2ЎўЎӯЎў°лФІOnөД°лҫ¶·ЦұрКЗr1Ўўr2ЎўЎӯЎўrnЈ¬Фтөұr1=2КұЈ¬r2016= Ј®
xПаЗРЈ¬Йи°лФІO1Ўў°лФІO2ЎўЎӯЎў°лФІOnөД°лҫ¶·ЦұрКЗr1Ўўr2ЎўЎӯЎўrnЈ¬Фтөұr1=2КұЈ¬r2016= Ј®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЈЁ1Ј©ОКМвЈәИзНј1Ј¬ФЪЛДұЯРОABCDЦРЈ¬өгPОӘABЙПТ»өгЈ¬ЎПDPC=ЎПA=ЎПB=90ЎгЈ®ЗуЦӨЈәAD![]() BC=AP
BC=AP![]() BPЈ®
BPЈ®
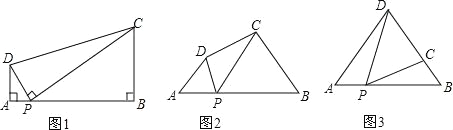
ЈЁ2Ј©МҪҫҝЈәИзНј2Ј¬ФЪЛДұЯРОABCDЦРЈ¬өгPОӘABЙПТ»өгЈ¬өұЎПDPC=ЎПA=ЎПB=ҰИКұЈ¬ЙПКцҪбВЫКЗ·сТАИ»іЙБўЈҝЛөГчАнУЙЈ®
ЈЁ3Ј©УҰУГЈәЗлАыУГЈЁ1Ј©ЈЁ2Ј©»сөГөДҫӯСйҪвҫцОКМвЈә
ИзНј3Ј¬ФЪЎчABDЦРЈ¬AB=12Ј¬AD=BD=10Ј®өгPТФГҝГл1ёцөҘО»іӨ¶ИөДЛЩ¶ИЈ¬УЙөгAіц·ўЈ¬СШұЯABПтөгBФЛ¶ҜЈ¬ЗТВъЧгЎПDPC=ЎПAЈ®ЙиөгPөДФЛ¶ҜКұјдОӘtЈЁГлЈ©Ј¬өұТФDОӘФІРДЈ¬ТФDCОӘ°лҫ¶өДФІУлABПаЗРЈ¬ЗуtөДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com