
����Ŀ��ij�̳�����һ�ֳɱ�Ϊÿ��60Ԫ�ķ�װ���涨�����ڼ����۵��۲����ڳɱ����ۣ��һ������ø���45%�����������֣�������y�����������۵���x��Ԫ������һ�κ���y=kx+b����x=65ʱ��y=55��x=75ʱ��y=45��
��1����һ�κ���y=kx+b�ı���ʽ��
��2�������̳��������ΪWԪ����д������W�����۵���x֮��Ĺ�ϵʽ�����۵��۶�Ϊ����Ԫʱ���̳��ɻ�����������������Ƕ���Ԫ��
��3�������̳����������500Ԫ����ȷ�����۵���x�ķ�Χ��
���𰸡�
��1���⣺��������� ![]()
���k=��1��b=120��
����һ�κ����ı���ʽΪy=��x+120��
��2���⣺W=��x��60������x+120��
=��x2+180x��7200
=����x��90��2+900��
�������ߵĿ������£�
�൱x��90ʱ��W��x�����������
�����۵��۲����ڳɱ����ۣ��һ������ø���45%��
��60��x��60����1+45%����
��60��x��87��
�൱x=87ʱ��W=����87��90��2+900=891��
�൱���۵��۶�Ϊ87Ԫʱ���̳��ɻ������������������891Ԫ��
��3���⣺��W��500����500�ܩ�x2+180x��7200��
�����ã�x2��180x+7700��0��
������x2��180x+7700=0�Ľ�Ϊ x1=70��x2=110��
��x1=70��x2=110ʱ����Ϊ500Ԫ��������y=��x2+180x��7200�Ŀ������£�����Ҫʹ���̳����������500Ԫ�����۵���Ӧ��70Ԫ��110Ԫ֮�䣬
��60Ԫ/����x��87Ԫ/�������ԣ����۵���x�ķ�Χ��70Ԫ/����x��87Ԫ/����
����������1���г���Ԫһ�η�������k��b��ֵ�����һ�κ����ı���ʽ����2�����������W��x�ĺ�������ʽ���Ƴ���x=87ʱ�̳��ɻ���������3����w=500�Ƴ�x2��180x+7700=0���x��ֵ���ɣ�


 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
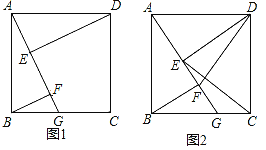
����Ŀ����ͼ1���ı���ABCD�������Σ���G��BC��������һ�㣬DE��AG�ڵ�E��BF��DE�ҽ�AG�ڵ�F��
��1����֤��DE=AF��
��2����AB=4��BG=3����AF�ij���
��3����ͼ2������DF��CE���ж��߶�DF��CE��λ�ù�ϵ��֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м���������4����ͬ��С�������ɵģ���������ͼ������ͼ��ͬ���ǣ� ��
A.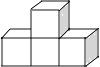
B.
C.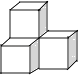
D.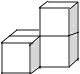
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
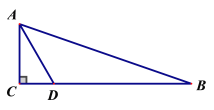
��![]() ����DΪBC����һ�㣬��BD=2AD������
����DΪBC����һ�㣬��BD=2AD������![]() ���ܳ����������ţ���
���ܳ����������ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
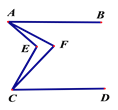
����Ŀ����ͼ����֪AB��CD,��EAF =![]() ��EAB,��ECF=
��EAB,��ECF=![]() ��ECD ,���AFC���AEC֮���������ϵ��_____________________________
��ECD ,���AFC���AEC֮���������ϵ��_____________________________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=��2x+10��x�ᣬy���ཻ��A��B���㣬��C�������ǣ�8��4��������AC��BC��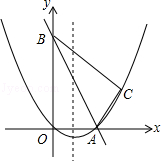
��1�����O��A��C����������ߵĽ���ʽ�����жϡ�ABC����״��
��2������P�ӵ�O��������OB��ÿ��2����λ���ȵ��ٶ����B�˶���ͬʱ������Q�ӵ�B��������BC��ÿ��1����λ���ȵ��ٶ����C�˶����涨����һ�����㵽��˵�ʱ����һ������Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�룬��tΪ��ֵʱ��PA=QA��
��3���������ߵĶԳ����ϣ��Ƿ���ڵ�M��ʹ��A��B��MΪ������������ǵ��������Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ��κ���y=x2��2mx��3�������н��ۣ� ������ͼ����x�����������㣻
�����������ͼ������ƽ��3����λ���ԭ�㣬��m=1��
�������x=2ʱ�ĺ���ֵ��x=8ʱ�ĺ���ֵ��ȣ���m=5��
����һ����ȷ�Ľ����� �� ��������Ϊ��ȷ���۵���Ŷ����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
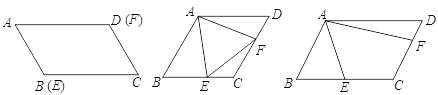
����Ŀ����E��F�ֱ�����ABCD�ı�BC��CD�ϵĵ㣬��EAF��60�㣬AF��4
(1) ��AB��2����E���B����F���D�ֱ��غϣ���ƽ���ı���ABCD�����
(2) ��AB��BC����B����EAF��60������֤����AEFΪ�ȱ�������
(3) ��BE��CE��CF��2DF��AB��3��ֱ��д��AE�ij��ȣ���������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧ������ѧ���п�չ��ɳ�����������������������������Ŀ�Ļ��Ϊ�˽�ѧ����������Ŀ��ϲ���������������˸�Уm��ѧ����ϲ����һ����Ŀ��ÿ��ѧ����ѡ��ֻ��ѡ�����ֻ��Ŀ��һ�֣����������������Ƴ����µIJ�������ͳ��ͼ����
ѧ����ϲ���Ļ��Ŀ������ͳ�Ʊ�
��Ŀ | ѧ���������� | �ٷֱ� |
��ɳ�� | 20 | 10% |
������ | 60 | p% |
������ | n | 40% |
����� | 40 | 20% |
����ͼ�����ṩ����Ϣ������������⣺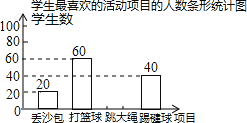
��1��m= �� n= �� p=��
��2�������������Ϣֱ�Ӳ�ȫ����ͳ��ͼ��
��3�����ݳ�����������������Ƹ�У2000��ѧ�����ж�����ѧ����ϲ����������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com