
【题目】宽与长的比是 ![]() (约为0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC的中点E,F,连接EF,DF,作∠DFC,的平分线,交AD的延长线于点H,作HG⊥BC,交I3C的延长线于点G,则下列矩形是黄金矩形的是( )
(约为0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC的中点E,F,连接EF,DF,作∠DFC,的平分线,交AD的延长线于点H,作HG⊥BC,交I3C的延长线于点G,则下列矩形是黄金矩形的是( )
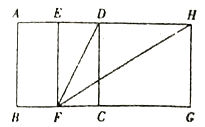
A. 矩形ABFE B. 矩形EFCD C. 矩形EFGH D. 矩形DCGH
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙![]() 与菱形
与菱形![]() 在平面直角坐标系中,点
在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,且点
轴上,且点![]() 在点
在点![]() 的右侧.
的右侧.


(![]() )求菱形
)求菱形![]() 的周长.
的周长.
(![]() )若⊙
)若⊙![]() 沿
沿![]() 轴向右以每秒
轴向右以每秒![]() 个单位长度的速度平移,菱形
个单位长度的速度平移,菱形![]() 沿
沿![]() 轴向左以每秒
轴向左以每秒![]() 个单位长度的速度平移,设菱形移动的时间为(
个单位长度的速度平移,设菱形移动的时间为(![]() 秒),当⊙
秒),当⊙![]() 与
与![]() 相切,且切点为
相切,且切点为![]() 的中点时,连接
的中点时,连接![]() ,求
,求![]() 的值及
的值及![]() 的度数.
的度数.
(![]() )在(
)在(![]() )的条件下,当点
)的条件下,当点![]() 与
与![]() 所在的直线的距离为
所在的直线的距离为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,AD∥BC,连接对角线AC.
(1)在边AD上确定一点E,使EA=EC;在边BC上确定一点F,使FA=FC;(尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,连接AF,CE.求证:四边形AFCE是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图象经过第一、二、三象限,且与反比例函数图象相交于
的图象经过第一、二、三象限,且与反比例函数图象相交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
, ![]() .且点
.且点![]() 横坐标是点
横坐标是点![]() 纵坐标的2倍.
纵坐标的2倍.
(1)求反比例函数的解析式;
(2)设点![]() 横坐标为
横坐标为![]() ,
, ![]() 面积为
面积为![]() ,
,
求![]() 与
与![]() 的函数关系式,并求出自变量的取值范围.
的函数关系式,并求出自变量的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高高地路灯挂在路边的上方,高傲而明亮,小明拿着一根![]() 米长的竹竿,想量一量路灯的高度,直接量是不可能的,于是,他走到路灯旁的一个地方,竖起竹竿,这时,他量了一下竹竿的影长正好是
米长的竹竿,想量一量路灯的高度,直接量是不可能的,于是,他走到路灯旁的一个地方,竖起竹竿,这时,他量了一下竹竿的影长正好是![]() 米,他沿着影子的方向走,向远处走出两根竹竿的长度(即
米,他沿着影子的方向走,向远处走出两根竹竿的长度(即![]() 米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即
米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即![]() 米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,原来路灯有
米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,原来路灯有![]() 米高呀!”(如图所示)同学们,你觉得小明的判断对吗?
米高呀!”(如图所示)同学们,你觉得小明的判断对吗?
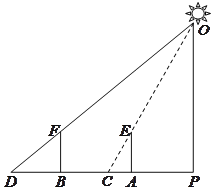
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F,下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F为定值.其中结论正确的有( )

A. 4个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量出楼房AC的高度,从距离楼底C处60![]() 米的点D(点D与楼底C在同一水平上)出发,沿斜面坡度为i=l:
米的点D(点D与楼底C在同一水平上)出发,沿斜面坡度为i=l: ![]() 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53![]() ,求楼房AC的高度(参考数据:sin53
,求楼房AC的高度(参考数据:sin53![]() =
=![]() , cos53
, cos53![]() =
=![]() , tan53
, tan53![]() =
=![]() ,
, ![]() ≈1.732,结果精确到0.1米)
≈1.732,结果精确到0.1米)
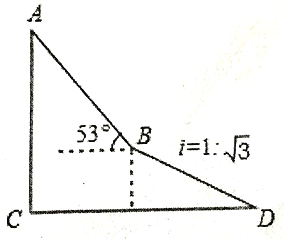
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2.
(1)求实数k的取值范围.
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]()
(1)请直接写出方程![]() 的所有正整数解
的所有正整数解
(2)若方程组的解满足x+y=0,求m的值
(3)无论实数m取何值,方程x-2y+mx+5=0总有一个固定的解,请直接写出这个解?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com