
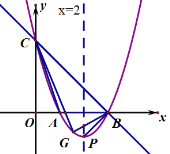
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点B、C,经过B、C两点的抛物线
轴分别相交于点B、C,经过B、C两点的抛物线![]() 与
与![]() 轴的另一个交点为A,顶点为P,且对称轴为直线
轴的另一个交点为A,顶点为P,且对称轴为直线![]() 。点G是抛物线
。点G是抛物线![]() 位于直线
位于直线![]() 下方的任意一点,连接PB、GB、GC、AC .
下方的任意一点,连接PB、GB、GC、AC .
(1)求该抛物线的解析式;
(2)求△GBC面积的最大值;
(3)连接AC,在![]() 轴上是否存在一点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由。
轴上是否存在一点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由。
【答案】(1)![]() ; (2)当时
; (2)当时![]() ,
,![]() 面积的取最大值
面积的取最大值![]() ; (3)在x轴上存在两点Q1(0,0),Q2(
; (3)在x轴上存在两点Q1(0,0),Q2(![]() ,0),能使得以点P,B,Q为顶点的三角形与△ABC相似.
,0),能使得以点P,B,Q为顶点的三角形与△ABC相似.
【解析】
(1)根据二次函数的对称性,已知对称轴的解析式以及B点的坐标,即可求出A的坐标,利用抛物线过A、B、C三点,可用待定系数法来求函数的解析式;
(2)过![]() 作
作![]() ∥
∥![]() 轴交
轴交![]() 于点
于点![]() .设点
.设点![]()
![]() ,则点
,则点![]() ,列出关于△GBC面积的解析式,利用二次函数的性质求解即可;
,列出关于△GBC面积的解析式,利用二次函数的性质求解即可;
(3)本题要先根据抛物线的解析式求出顶点P的坐标,然后求出BP的长,进而分三情况进行讨论:①当![]() ,∠PBQ=∠ABC=45°时;②当
,∠PBQ=∠ABC=45°时;②当![]() ,∠QBP=∠ABC=45°时;③当Q在B点右侧,即可得出∠PBQ≠∠BAC,因此此种情况是不成立的,综上所述即可得出符合条件的Q的坐标.
,∠QBP=∠ABC=45°时;③当Q在B点右侧,即可得出∠PBQ≠∠BAC,因此此种情况是不成立的,综上所述即可得出符合条件的Q的坐标.
(1)∵直线y=﹣x+3与x轴相交于点B、点C,
∴当y=0时,x=3;当x=0时,y=3.
∴点B的坐标为(3,0),点C的坐标为(0,3),
又∵抛物线过x轴上的A,B两点,且对称轴为x=2,
∴点A的坐标为(1,0).
又∵抛物线y=ax2+bx+c过点A(1,0),B(3,0),C(0,3),
 , 解得:
, 解得: ,
,
∴该抛物线的解析式为:![]() ;
;
(2)如图,过![]() 作
作![]() ∥
∥![]() 轴交
轴交![]() 于点
于点![]() .
.

设点![]()
![]() ,则点
,则点![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
∵![]() ,
,
∴ 当时![]() ,
,![]() 面积的取最大值
面积的取最大值![]() .
.
(3)如图,

由y=x2﹣4x+3=(x﹣2)2﹣1,得顶点P(2,﹣1),
设抛物线的对称轴交x轴于点M,
∵在Rt△PBM中,PM=MB=1,
∴∠PBM=45°,PB=![]() .
.
由点B(3,0),C(0,3)易得OB=OC=3,在等腰直角三角形OBC中,∠ABC=45°,
由勾股定理,得BC=![]() .
.
假设在x轴上存在点Q,使得以点P,B,Q为顶点的三角形与△ABC相似.
①当![]() ,∠PBQ=∠ABC=45°时,△PBQ∽△ABC.
,∠PBQ=∠ABC=45°时,△PBQ∽△ABC.
即![]() ,
,
解得:BQ=3,
又∵BO=3,
∴点Q与点O重合,
∴Q1的坐标是(0,0).
②当![]() ,∠QBP=∠ABC=45°时,△QBP∽△ABC.
,∠QBP=∠ABC=45°时,△QBP∽△ABC.
即![]() ,
,
解得:QB=![]() .
.
∵OB=3,
∴OQ=OB﹣QB=3﹣![]() ,
,
∴Q2的坐标是(![]() ,0).
,0).
③当Q在B点右侧,
则∠PBQ=![]() =135°,∠BAC<135°,
=135°,∠BAC<135°,
故∠PBQ≠∠BAC.
则点Q不可能在B点右侧的x轴上,
综上所述,在x轴上存在两点Q1(0,0),Q2(![]() ,0),能使得以点P,B,Q为顶点的三角形与△ABC相似.
,0),能使得以点P,B,Q为顶点的三角形与△ABC相似.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知函数y=﹣![]() (x+2)2﹣2
(x+2)2﹣2
(1)指出函数图象的开口方向是 ,对称轴是 ,顶点坐标为 .
(2)当x 时,y随x的增大而减小;
(3)怎样移动抛物线y=﹣![]() x2就可以得到抛物线y=﹣
x2就可以得到抛物线y=﹣![]() (x+2)2﹣2.
(x+2)2﹣2.
查看答案和解析>>
科目:初中数学 来源: 题型:
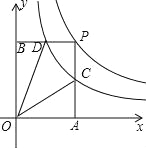
【题目】如图是函数y=![]() 与函数y=
与函数y=![]() 在第一象限内的图象,点P是y=
在第一象限内的图象,点P是y=![]() 的图象上一动点,PA⊥x轴于点A,交y=
的图象上一动点,PA⊥x轴于点A,交y=![]() 的图象于点C,PB⊥y轴于点B,交y=
的图象于点C,PB⊥y轴于点B,交y=![]() 的图象于点D.
的图象于点D.
(1)求证:D是BP的中点;
(2)求四边形ODPC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程S(km)与北京时间t(时)的函数图象如图所示.根据图象得到小亮结论,其中错误的是( )
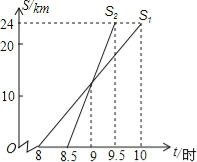
A. 小亮骑自行车的平均速度是12km/h
B. 妈妈比小亮提前0.5小时到达姥姥家
C. 妈妈在距家12km处追上小亮
D. 9:30妈妈追上小亮
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直线y=kx+k交x轴负半轴于点A,交y轴正半轴于点B,且AB=2
(1)求k的值;
(2)点P从A出发,以每秒1个单位的速度沿射线AB运动,过点P作直线AB的垂线交x轴于点Q,连接OP,设△PQO的面积为S,点P运动时间为t,求S与t的函数关系式,并直接写出t的取值范围;
(3)在(2)的条件下,当P在AB的延长线上,若OQ+AB=![]() (BQ﹣OP),求此时直线PQ的解析式.
(BQ﹣OP),求此时直线PQ的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且AB=AC,延长BC至点D,使CD=CA,连接AD交⊙O与点E,连接BE,CE.
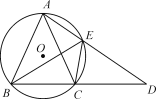
(1)求证:△ABE≌△CDE;
(2)填空:
①当∠ABC的度数为______时,四边形AOCE是菱形;
②若AE=![]() ,AB=2
,AB=2![]() ,则DE的长为______.
,则DE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阳阳超市以每件10元的价格购进了一批玩具,定价为20元时,平均每天可售出80个.经调查发现,玩具的单价每降1元,每天可多售出40个;玩具的单价每涨1元,每天要少售出5个.如何定价才能使每天的利润最大?求出此时的最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com