
在△ABC中,若AB=15,AC=13,高AD=12,则△ABC的周长是( )。
A.42 B.32 C.42或32 D.37或33
科目:初中数学 来源:2014-2015学年江苏省八年级上学期期中数学试卷(解析版) 题型:解答题
【问题提出】学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 ,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角,求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)
(4)∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,若 ,则△ABC≌△DEF.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏盐城东台苏东双语学校初二上第一次检测二数学卷(解析版) 题型:解答题
①如图:A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站, 将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在 图中确定该点(保留作图痕迹)
②如图:某地有两所大学M、N和两条相交叉的公路a、b,现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等。你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案;


查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏盐城东台苏东双语学校初二上第一次检测二数学卷(解析版) 题型:选择题
已知等腰三角形一腰上的高线与另一腰的夹角为 ,那么这个等腰三角形的顶角等于( )
A.15°或75° B.140° C.40° D.140°或40° ( )
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏徐州丰县中学八年级上学期第一次质检数学试卷(解析版) 题型:解答题
已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.试说明△ABC是等腰三角形.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏徐州丰县中学八年级上学期第一次质检数学试卷(解析版) 题型:选择题
在△ABC内一点P满足PA=PB=PC,则点P一定是△ABC( )
A.三条角平分线的交点
B.三边垂直平分线的交点
C.三条高的交点
D.三条中线的交点
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广西邕宁区蒲庙镇二中八年级上学期期中考试数学试卷(解析版) 题型:填空题
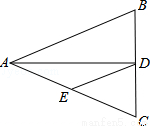
如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com