
 y=
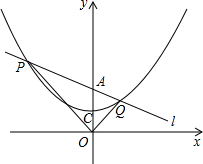
y= x2+h的图象交于不同的两点P、Q.
x2+h的图象交于不同的两点P、Q. x2+h经过点C(0,1),
x2+h经过点C(0,1), ×0+h=1,
×0+h=1, x2+1上的点,P(a,
x2+1上的点,P(a, a2+1)、Q(b,
a2+1)、Q(b, b2+1)(a<0<b)
b2+1)(a<0<b) a2+1=ak+2…①
a2+1=ak+2…① b2+1=bk+2…②
b2+1=bk+2…② (a2b-b2a)+b-a=2(b-a),
(a2b-b2a)+b-a=2(b-a), ;
; OA•|xQ-xP|=
OA•|xQ-xP|= •OA•|-
•OA•|- -a|=(-
-a|=(- )+(-a)≥2•
)+(-a)≥2•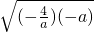 =4
=4 =-a,即|a|=|b|(P、Q关于y轴对称)时,△POQ的面积最小;
=-a,即|a|=|b|(P、Q关于y轴对称)时,△POQ的面积最小;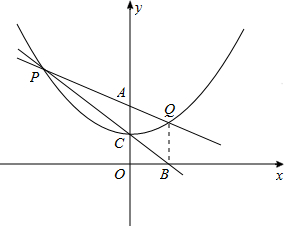
 x2+1上的点,P(a,
x2+1上的点,P(a, a2+1)、Q(b,
a2+1)、Q(b, b2+1)(a<0<b)
b2+1)(a<0<b) a2+1=ak1+1,得k1=
a2+1=ak1+1,得k1= a,
a, ax+1.
ax+1. ,
,


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )查看答案和解析>>
科目:初中数学 来源: 题型:
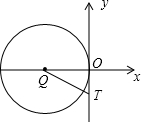
 (2012•集美区一模)如图,O为坐标原点,小明在运动场练习踢足球,足球在点O处飞出,落在点B处,已知足球经过的路线是抛物线y=-
(2012•集美区一模)如图,O为坐标原点,小明在运动场练习踢足球,足球在点O处飞出,落在点B处,已知足球经过的路线是抛物线y=-| 1 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
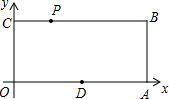 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上以每秒1个单位的速度由C向B运动.
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上以每秒1个单位的速度由C向B运动.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图:0为坐标原点,点A(1,4)和点B(a,1)均在反比例函数y=
如图:0为坐标原点,点A(1,4)和点B(a,1)均在反比例函数y=| m | x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com