
【题目】如图在平面直角坐标系xOy中,反比例函数y1= ![]() (x>0)的图象与一次函数y2=kx-k的图象的交点为A(m,2).
(x>0)的图象与一次函数y2=kx-k的图象的交点为A(m,2).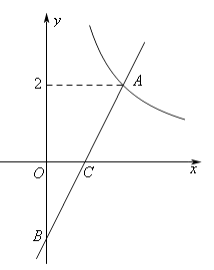
(1)求一次函数的解析式;
(2)观察图像,直接写出使y1≥y2的x的取值范围.
(3)设一次函数y=kx-k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是4,请写出点P的坐标.
【答案】
(1)解:将A(m,2)代入 ![]() (x>0)得,m=2,则A点坐标为A(2,2),将A(2,2)代入y=kx-k得,2k-k=2,解得k=2,则一次函数解析式为y=2x-2
(x>0)得,m=2,则A点坐标为A(2,2),将A(2,2)代入y=kx-k得,2k-k=2,解得k=2,则一次函数解析式为y=2x-2
(2)解:当0<x≤2时, y1≥y2 ;
(3)解:∵一次函数y=2x-2与x轴的交点为C(1,0),与y轴的交点为B(0,-2),S△ABP=S△ACP+S△BPC,
∴ ![]() ×2CP+
×2CP+ ![]() ×2CP=4,解得CP=2,则P点坐标为(3,0),(-1,0)
×2CP=4,解得CP=2,则P点坐标为(3,0),(-1,0)
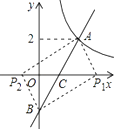
【解析】(1)首先把A点的坐标代入反比例函数的解析式求出A点的坐标,再把A点的坐标代入一次函数的解析式求出k的值,从而得出一次函数的解析式;
(2)利用图像求不等式的解集,就是弄清谁大谁小,谁大就看谁的图像在上方的时候的自变量的取值范围;
(3)求出一次函数y=2x-2与x轴的交点C的坐标,与y轴的交点B的坐标,利用S△ABP=S△ACP+S△BPC,列出方程求出CP的长,从而得到P点的坐标。
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,AC∥BD,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,那么图中全等的三角形有( )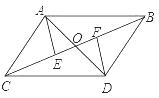
A.5对
B.6对
C.7对
D.8对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四组线段中,可以构成直角三角形的是( )
A.4cm、5cm、6cm
B.1cm、 ![]() cm、3cm
cm、3cm
C.2cm、3cm、4cm
D.1.5cm、2cm、2.5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为边在AD的右侧作正方形ADEF,连接CF.
(1)观察猜想:如图(1),当点D在线段BC上时,
①BC与CF的位置关系是: ;
②BC、CD、CF之间的数量关系为: (将结论直接写在横线上)
(2)数学思考:如图(2),当点D在线段CB的延长线上时,上述①、②中的结论是否仍然成立?若成立,请给予证明,若不成立,请你写出正确结论再给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利群商厦对销量较大的A、B、C三种品牌的纯牛奶进行了问卷调查,共发放问卷300份(问卷由单选和多选题组成),对收回的265份问卷进行了整理,部分数据如下:
(1)最近一次购买各品牌纯牛奶用户比例如图:

(2)用户对各品牌纯牛奶满意情况汇总如下表:
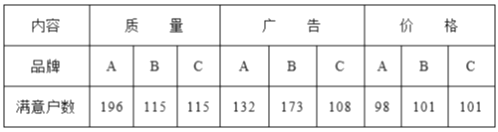
结合上述信息回答下列问题:
①A品牌牛奶的主要竞争优势是什么?请简要说明理由.
②广告对用户选择品牌有影响吗?请简要说明理由.
③你对厂家C有何建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
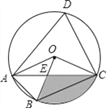
【题目】如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2![]() ,则图中阴影部分面积是_____(结果保留π和根号)
,则图中阴影部分面积是_____(结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
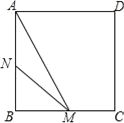
【题目】如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )
A. 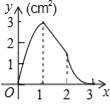 B.
B.  C.
C. 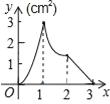 D.
D. 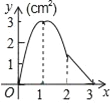
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com