

分析 (1)根据同角的余角相等可以得:∠ABD=∠NAC;
(2)如图2作辅助线,构建全等三角形,利用ASA证明△ECN≌△PCN,得∠APC=∠NEC,再利用SAS证明△ECN≌△PCN,所以∠APC=∠NEC,则∠ADB=∠NEC,利用等角对等边得:FD=FE;
(3)如图1,同理可证明FD=FE,则△FED为等腰三角形.
解答  解:(1)如图1,∵∠BAC=90°,
解:(1)如图1,∵∠BAC=90°,
∴∠NAC+∠BAN=90°,
∵AM⊥BD,
∴∠AMB=90°,
∴∠ABD+∠BAN=90°,
∴∠ABD=∠NAC;
(2)FD=FE,理由是:
如图2,过C作CP⊥AC,交AN的延长线于P,
∴∠ACP=∠BAC=90°,
∵AB=AC,∠NAC=∠ABD,
∴△APC≌△BDA,
∴AD=PC,∠ADB=∠APC,
由题意得:AD=EC,
∴AD=EC=PC,
∵AB=AC,∠BAC=90°,
∴∠ACB=45°,
∴∠PCN=45°,
∴∠ACB=∠PCN,
∵NC=NC,
∴△ECN≌△PCN,
∴∠APC=∠NEC,
∴∠ADB=∠NEC,
∴FD=FE;
(3)如图1,过C作CP⊥AC,交AN的延长线于P,
∴∠ACP=∠BAC=90°,
∵AB=AC,∠NAC=∠ABD,
∴△APC≌△BDA,
∴AD=PC,∠ADB=∠APC,
由题意得:AD=EC,
∴AD=EC=PC,
∵AB=AC,∠BAC=90°,
∴∠ACB=45°,
∴∠PCN=45°,
∴∠ACB=∠PCN,
∵NC=NC,
∴△ECN≌△PCN,
∴∠APC=∠NEC,
∴∠ADB=∠NEC,
∵∠ADB=∠FDE,∠NEC=∠FED,
∴∠FDE=∠FED,
∴FD=FE;
∴△FED为等腰三角形.
点评 本题是三角形的综合题,考查了等腰直角三角形、等腰三角形、全等三角形的性质和判定,本题主要利用证明两个三角形全等来证明边相等或角相等,从而解决问题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题

| 图形编号 | (1) | (2) | (3) | (4) | … | (10) | … | (100) |
| 图中座位总数 | 6 | 10 | 14 | 18 | … | 42 | … | 402 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
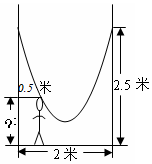 如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为多少米?
如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com