
 如图,已知AB是⊙O的直径,BC⊥AB,连接OC,弦AD∥OC,直线CD交BA的延长线于点E.
如图,已知AB是⊙O的直径,BC⊥AB,连接OC,弦AD∥OC,直线CD交BA的延长线于点E.分析 (1)首选连接OD,易证得△COD≌△COB(SAS),然后由全等三角形的对应角相等,求得∠CDO=90°,即可证得直线CD是⊙O的切线;
(2)由△COD≌△COB可得CD=CB,即可得DE=2CD,易证得△EDA∽△ECO,然后由相似三角形的对应边成比例,求得AD:OC的值;
(3)根据切割线定理得出EB,即可求得AB的长.
解答 (1)证明:连结DO.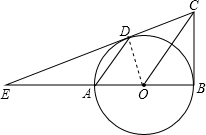
∵AD∥OC,
∴∠DAO=∠COB,∠ADO=∠COD.
又∵OA=OD,
∴∠DAO=∠ADO,
∴∠COD=∠COB.
在△COD和△COB中,
$\left\{\begin{array}{l}{CO=CO}\\{∠COD=∠COB}\\{OD=OB}\end{array}\right.$,
∴△COD≌△COB(SAS)
∴∠CDO=∠CBO=90°.
又∵点D在⊙O上,
∴CD是⊙O的切线.
(2)解:∵△COD≌△COB.
∴CD=CB.
∵DE=2BC,
∴ED=2CD.
∵AD∥OC,
∴△EDA∽△ECO.
∴$\frac{AD}{OC}$=$\frac{2}{3}$.
(3)∵CD是⊙O的切线,
∴ED2=EA•EB,
∵ED=4,EA=2,
∴42=2EB,
∴EB=8,
∴AB=EB-EA=8-2=6.
点评 此题考查了切线的判定、全等三角形的判定与性质以及相似三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
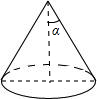 如图,圆锥的底面半径为3,侧面积为18π,设圆锥的母线与高的夹角为α,则tanα的值是( )
如图,圆锥的底面半径为3,侧面积为18π,设圆锥的母线与高的夹角为α,则tanα的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届四川省广安市岳池县九年级第二次诊断考试数学试卷(解析版) 题型:判断题
广安某网站调查,2016年网民们最关注的热点话题分别有:消费、教育、环保、反腐及其它共五类.根据调查的部分相关数据,绘制的统计图表如下:
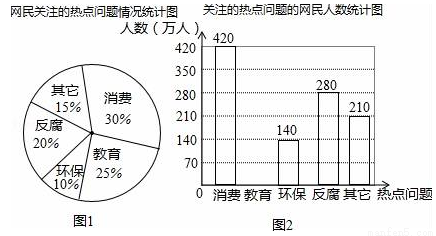
根据以上信息解答下列问题:
(1)请补全条形统计图并在图中标明相应数据;
(2)若广安市约有900万人口,请你估计最关注环保问题的人数约为多少万人?
(3)在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,则抽取的两人恰好是甲和乙的概率是多少.
查看答案和解析>>
科目:初中数学 来源:2017届四川省广安市岳池县九年级第二次诊断考试数学试卷(解析版) 题型:单选题
若关于x 的一元二次方程(m﹣2)2x2+(2m+1)x+1=0有解,那么m的取值范围是( )
A. 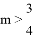 B.
B. 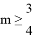 C.
C. 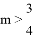 且m≠2 D.
且m≠2 D. 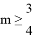 且m≠2
且m≠2
查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省杭州市萧山区戴村片八年级3月月考数学试卷(解析版) 题型:填空题
如果关于x的一元二次方程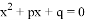 的两根分别为
的两根分别为 ,
,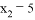 ,那么这个一元二次方程是______.
,那么这个一元二次方程是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com