Question

【题目】如图，四边形ABCD是矩形，点E在CD边上，点F在DC延长线上，AE=BF．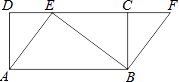
（1）求证：四边形ABFE是平行四边形；
（2）若∠BEF=∠DAE，AE=3，BE=4，求EF的长．

Answer 1

【答案】
（1）证明：∵四边形ABCD是矩形，

∴AD=BC，∠D=∠BCD=90°．

∴∠BCF=180°﹣∠BCD=180°﹣90°=90°．

∴∠D=∠BCF．在Rt△ADE和Rt△BCF中，

∴Rt△ADE≌Rt△BCF．

∴∠1=∠F．

∴AE∥BF．

∵AE=BF，

∴四边形ABFE是平行四边形

（2）解：∵∠D=90°，

∴∠DAE+∠1=90°．

∵∠BEF=∠DAE，

∴∠BEF+∠1=90°．

∵∠BEF+∠1+∠AEB=180°，

∴∠AEB=90°．

在Rt△ABE中，AE=3，BE=4，

AB= ．

∵四边形ABFE是平行四边形，

∴EF=AB=5

【解析】（1）欲证明四边形ABFE是平行四边形，只要证明AE∥BF，EF∥AB即可．（2）先证明△AEB是直角三角形，再根据勾股定理计算即可．
【考点精析】通过灵活运用平行四边形的判定与性质和矩形的性质，掌握若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积；矩形的四个角都是直角，矩形的对角线相等即可以解答此题．