
如图,直线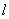 :
: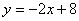 分别与
分别与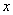 轴、
轴、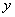 轴交于A、B两点,点C线段AB上,作CD⊥x轴于D, CD=2OD, 点E线段OB上,且AE=BE;
轴交于A、B两点,点C线段AB上,作CD⊥x轴于D, CD=2OD, 点E线段OB上,且AE=BE;
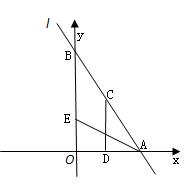
(1)填空:点C的坐标为( , );点E的坐标为( , );
(2)直线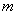 过点E,且将△AOB分成面积比为1:2的两部分,求直线
过点E,且将△AOB分成面积比为1:2的两部分,求直线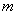 的表达式;
的表达式;
(3)点P在x轴上运动,
①当PC+PE取最小值时,求点P的坐标及PC+PE的最小值;
②当PC-PE取最大值时,求点P的坐标及PC-PE的最大值;
(1)点C( 2 , 4 );点E( 0 , 3 );
(2)直线m的表达式为: 或
或
(3)① ;②
;②
【解析】
分析:(1)根据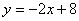 求出点A,B的坐标,A(4,0),B(0,8),所以OA=4,OB=8,设OD=m,则CD=2OD=2m,因为 CD⊥x轴,所以点C的坐标是(m,2m)代入
求出点A,B的坐标,A(4,0),B(0,8),所以OA=4,OB=8,设OD=m,则CD=2OD=2m,因为 CD⊥x轴,所以点C的坐标是(m,2m)代入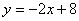 可求出点C的坐标,设OE=x,则AE=BE=8-x,在△OAE中,根据勾股定理可求出x的值,从而可得点E的坐标;
可求出点C的坐标,设OE=x,则AE=BE=8-x,在△OAE中,根据勾股定理可求出x的值,从而可得点E的坐标;
(2)设直线m的表达式为 ,然后分情况讨论
,然后分情况讨论
(3)①求出点E关于X轴的对称点E′坐标,然后求直线C E′与x轴的交点,即为点P;②直线CE与与x轴的交点即为点P.
解:(1)点C( 2 , 4 );点E( 0 , 3 );
(2)设直线m的表达式为
①如图:

当 时,
时,
得FH= ,将
,将 代入
代入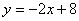 得
得
将点F( ,
, )代入
)代入 得
得 ,
,
所以直线m的表 达式为
达式为
②如图:

当 时,
时, ,
,
得ON= ,将点N(
,将点N( ,
, )代入
)代入 得
得 ,
,
所以直线m的表达式为
综上,直线m的表达式为: 或
或
(3)①如图:

E关于X轴的对称点E′坐标为(0,-3),
设直线CE′的表达式为 代入C(2,4)得;
代入C(2,4)得; ,所以
,所以
将 代入
代入 得
得
所以P的坐标为
作E′Q⊥CD于Q,则E′Q=OD=2,CQ=7
所以PC+PE的最小值= CE′= =
=
②如图:

设直线CE的表达式为 ,与x轴相交为p,
,与x轴相交为p,
代入C(2,4),得 ,
,
所以 ,当
,当 时,
时, ;点P坐标为(-6,0),
;点P坐标为(-6,0),
作CR⊥y轴于R,则CR=OD=2,ER=1,
所以PC-PE的最 大值= CE=
大值= CE= =
=
【难度】较难


科目:初中数学 来源: 题型:
李明到离家2.1千米的学校参加初三联欢会,到学校时发现演出道具还放在家中,此时距联欢会开始还有42分钟,于是他立即匀速步行回家,在家拿道具用了1分钟,然后立即匀速骑自行车返回学校.已知李明骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.
(1)李明步行的速度(单位:米/分)是多少?
(2)李明能否在联欢会开始前赶到学校?
查看答案和解析>>
科目:初中数学 来源: 题型:
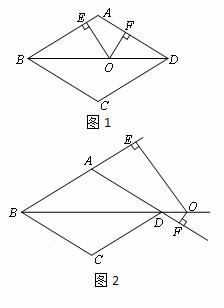
如图,在边长为10的菱形ABCD中,对角线BD=16,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)对角线AC的长是 ,菱形ABCD的面积是 ;
(2)如图1,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由;
(3)如图2,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由,若变化,请探究OE、OF之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com