
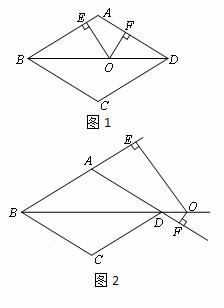
��ͼ���ڱ߳�Ϊ10������ABCD�У��Խ���BD��16����O��ֱ��BD�ϵĶ��㣬OE��AB��E��OF��AD��F��
��1���Խ���AC�ij��� ������ABCD������� ��
��2����ͼ1������O�ڶԽ���BD���˶�ʱ��OE��OF��ֵ�Ƿ����仯����˵�����ɣ�
��3����ͼ2������O�ڶԽ���BD���ӳ�����ʱ��OE��OF��ֵ�Ƿ����仯�������䣬��˵�����ɣ����仯����̽��OE��OF֮���������ϵ����˵�����ɣ�
��1��12��96 ��
��2��OE+OF=9��6�Ƕ�ֵ�����䣻
��3��OE+OF��ֵ�仯��OE��OF֮���������ϵΪ��OE-OF=9��6
��������
��������1������AC��BD�ཻ�ڵ�G���������εĶԽ����ഹֱƽ�����BG�������ù��ɶ�����ʽ���AG��Ȼ�����AC=2AG���㼴�ɵý⣻�ٸ������ε�������ڶԽ��߳˻���һ����ʽ���㼴�ɵý⣻
��2������AO������S��ABD=S��ABO+S��ADO��ʽ���㼴�ɵý⣻
��3������AO������S��ABD=S��ABO-S��ADO��ʽ�������ɵý⣮
�⣺��1����ͼ������AC��BD�ཻ�ڵ�G��

������ABCD��AC��BD��BG= BD=
BD= ��16=8��
��16=8��
�ɹ��ɶ����ã�AG= =6��
=6��
��AC=2AG=2��6=12��
����ABCD�����= AC•BD=
AC•BD= ��12��16=96��
��12��16=96��
�ʴ�Ϊ��12��96��
��2����ͼ������AO��

��
���ԣ� BD•AG=
BD•AG= AB•OE+
AB•OE+ AD•OF��
AD•OF��
�� ��16��6=
��16��6= ��10•OE+
��10•OE+ ��10•OF��
��10•OF��
���OE+OF=9��6�Ƕ�ֵ�����䣻
��3����ͼ������AO��

��
���ԣ� BD•AG=
BD•AG= AB•OE-
AB•OE- AD•OF��
AD•OF��
�� ��16��6=
��16��6= ��10•OE-
��10•OE- ��10•OF��
��10•OF��
���OE-OF=9��6���Ƕ�ֵ�����䣬
���ԣ�OE+OF��ֵ�仯��OE��OF֮���������ϵΪ��OE-OF=9��6��
���Ѷȡ�����


 ��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�Ӽס��������������и���ȡ10�꣬�ֱ������ǵĸ߶ȣ���λ��cm�����£�
�ף�25��41��40��37��22��14��19��39��21��42��
�ң�27��16��44��27��44��16��40��40��16��40��
�ʣ���1�����������糤�øߣ�
��2�����������糤�����룿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����֪A ��4��a����B ����2����4����һ�κ���y=kx+b��ͼ��ͷ���������y= ��ͼ��Ľ��㣮
��ͼ��Ľ��㣮
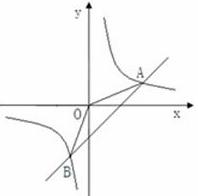
��1������������һ�κ����Ľ���ʽ��
��2�����A0B�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�ڡ�ABC�У�BC��a��AC��b��AB��c������C��90�㣬��ͼ��1��������ݹ��ɶ�������a2��b2��c2������ABC����ֱ�������Σ���ͼ��2���ͣ�3����������ȹ��ɶ������Բ���a2��b2��c2�Ĺ�ϵ����֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ֱ��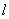 ��
��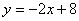 �ֱ���
�ֱ���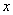 �ᡢ
�ᡢ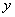 �ύ��A��B���㣬��C�߶�AB�ϣ���CD��x����D, CD=2OD, ��E�߶�OB��,��AE=BE��
�ύ��A��B���㣬��C�߶�AB�ϣ���CD��x����D, CD=2OD, ��E�߶�OB��,��AE=BE��
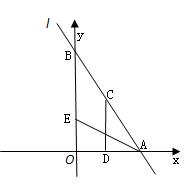
��1����գ���C������Ϊ�� �� ������E������Ϊ�� �� ����
��2��ֱ��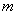 ����E���ҽ���AOB�ֳ������Ϊ1��2�������֣���ֱ��
����E���ҽ���AOB�ֳ������Ϊ1��2�������֣���ֱ��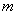 �ı���ʽ��
�ı���ʽ��
��3����P��x�����˶���
�ٵ�PC+PEȡ��Сֵʱ�����P�����꼰PC+PE����Сֵ��
�ڵ�PC-PEȡ���ֵʱ�����P�����꼰PC-PE�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����ֽƬABCD�ij�ADΪ4cm����ABΪ3cm���Ѿ���ֽƬƴ����ʹ���������A��C�غϣ�Ȼ��չ�������ۺ�EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��һ��ͯ��A����������ͯ����B����A��B����Ӱ��ľ���AC��BD�ij��ֱ�Ϊ200m��600m����CD��600m�����ǰ��ͯ��A������ǣ���ӱ���ˮ���ٸϻؼң���ô��ͯ����Ҫ�� m��
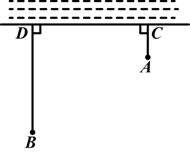
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com