
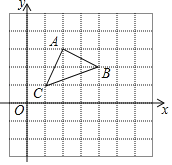
【题目】如图,平面直角坐标系中,△ABC的顶点都在正方形(每个小正方形边长为单位1)网格的格点上.
(1)△ABC的形状是_________(直接写答案);
(2)平移△ABC,若A对应的点A1坐标为(3,﹣1),画出△A1B1C1;
(3)画出△ABC绕点B顺时针旋转90°的△BA2C2并求出线段BC旋转过程扫过的面积.(结果保留π)
【答案】(1)等腰直角三角形;(2)画图见解析;(3)画图见解析,线段BC旋转过程扫过的面积为![]() .
.
【解析】
(1)根据网格特征,利用勾股定理可求出AC、BC、AB的长,再利用勾股定理的逆定理即可得答案;
(2)根据点A的平移过程可得出B、C两点的对应点B′、C′的坐标,顺次连接A′、B′、C′即可得△A1B1C1;
(3)利用网格特点和旋转的性质画出点A、B、C旋转后的对应点A2、B2、C2,即可得到△A2B2C2;利用扇形面积公式求出扇形BCC′的面积即可得答案.
(1)由勾股定理得:AC=![]() =
=![]() ,AB=
,AB=![]() =
=![]() ,BC=
,BC=![]() =
=![]() ,
,
∴AC=AB,
∴△ABC是等腰三角形,
∵(![]() )2=(
)2=(![]() )2+(
)2+(![]() )2,即BC2=AC2+AB2,
)2,即BC2=AC2+AB2,
∴△ABC是直角三角形,
∴△ABC是等腰直角三角形,
故答案为:等腰直角三角形
(2)由网格可知:A(2,3),B(4,2),C(1,1),
∵A对应的点A1坐标为(3,﹣1),
∴A1是点A先向下平移4个单位,再向右平移1个单位,
∴B1(5,-2),C1(2,-3),
∴△A1B1C1如图所示:
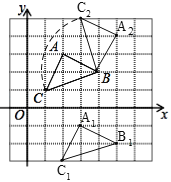
(3)由网格特征可得:△A2B2C2即为所求:
∵线段BC旋转过程扫过的面积为扇形BCC2的面积,∠CBC2=90°,BC=![]() ,
,
∴线段BC旋转过程扫过的面积为![]() =
=![]() .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】(2016山东省泰安市)某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)

根据图表提供的信息,下列结论错误的是( )

A. 这次被调查的学生人数为400人
B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中喜欢选修课E、F的人数分别为80,70
D. 喜欢选修课C的人数最少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示平面直角坐标系中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上.
(1)以O为旋转中心,将△ABC逆时针旋转90°,画出旋转后的△A1B1C1;
(2)画出△A1B1C1关于原点对称的△A2B2C2;
(3)若△ABC内有一点P(a,b),结果上面两次变换后点P在△A2B2C2中的对应点为P′,则点P′的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1,x2是关于x的一元二次方程![]() 的两实数根.
的两实数根.
(1)求m的范围;
(2)若![]() ,求m的值;
,求m的值;
(3)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.易证:CE=CF.

(1)在图1中,若G在AD上,且∠GCE=45°.试猜想GE,BE,GD三线段之间的数量关系,并证明你的结论.
(2)运用(1)中解答所积累的经验和知识,完成下面两题:
①如图2,在四边形ABCD中∠B=∠D=90°,BC=CD,点E,点G分别是AB边,AD边上的动点.若∠BCD=α,∠ECG=β,试探索当α和β满足什么关系时,图1中GE,BE,GD三线段之间的关系仍然成立,并说明理由.
②在平面直角坐标中,边长为1的正方形OABC的两顶点A,C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图3).设△MBN的周长为p,在旋转正方形OABC的过程中,p值是否有变化?若不变,请直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
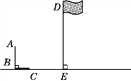
【题目】如图,九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画图步骤;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6 m,请你计算旗杆DE的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万达旅行社为吸引市民组团去黄山风景区旅游,推出了如下的收费标准:

宿州高铁新区组织员工去黄山风景区旅游,共支付给万达旅行社旅游费用27 000元,请问该单位这次共有多少员工去黄山风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
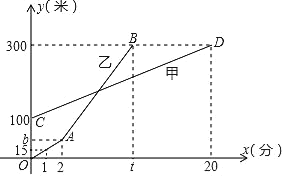
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?
查看答案和解析>>
科目:初中数学 来源: 题型:
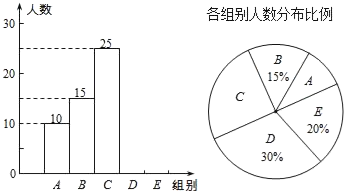
【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是 ;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com