
【题目】如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
【答案】
(1)
解:∵点A(﹣1,0)在抛物线y=﹣(x﹣1)2+c上,
∴0=﹣(﹣1﹣1)2+c,得c=4,
∴抛物线解析式为:y=﹣(x﹣1)2+4,
令x=0,得y=3,∴C(0,3);
令y=0,得x=﹣1或x=3,∴B(3,0).
(2)
解:△CDB为直角三角形.理由如下:
由抛物线解析式,得顶点D的坐标为(1,4).
如答图1所示,
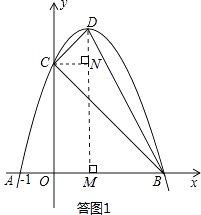
过点D作DM⊥x轴于点M,则OM=1,DM=4,BM=OB﹣OM=2.
过点C作CN⊥DM于点N,则CN=1,DN=DM﹣MN=DM﹣OC=1.
在Rt△OBC中,由勾股定理得:BC= ![]() ;
;
在Rt△CND中,由勾股定理得:CD= ![]() ;
;
在Rt△BMD中,由勾股定理得:BD= ![]() .
.
∵BC2+CD2=BD2,
∴△CDB为直角三角形(勾股定理的逆定理).
(3)
解:设直线BC的解析式为y=kx+b,∵B(3,0),C(0,3),
∴ ![]() ,
,
解得k=﹣1,b=3,
∴y=﹣x+3,
直线QE是直线BC向右平移t个单位得到,
∴直线QE的解析式为:y=﹣(x﹣t)+3=﹣x+3+t;
设直线BD的解析式为y=mx+n,∵B(3,0),D(1,4),
∴ ![]() ,
,
解得:m=﹣2,n=6,
∴y=﹣2x+6.
连接CQ并延长,射线CQ交BD于点G,则G( ![]() ,3).
,3).
在△COB向右平移的过程中:
(I) 当0<t≤ ![]() 时,如答图2所示:
时,如答图2所示:

设PQ与BC交于点K,可得QK=CQ=t,PB=PK=3﹣t.
设QE与BD的交点为F,则: ![]() ,解得
,解得 ![]() ,∴F(3﹣t,2t).
,∴F(3﹣t,2t).
S=S△QPE﹣S△PBK﹣S△FBE= ![]() PEPQ﹣
PEPQ﹣ ![]() PBPK﹣
PBPK﹣ ![]() BEyF=
BEyF= ![]() ×3×3﹣
×3×3﹣ ![]() (3﹣t)2﹣
(3﹣t)2﹣ ![]() t2t=
t2t= ![]() t2+3t;
t2+3t;
(II) 当 ![]() <t<3时,如答图3所示:
<t<3时,如答图3所示:

设PQ分别与BC、BD交于点K、点J.
∵CQ=t,
∴KQ=t,PK=PB=3﹣t.
直线BD解析式为y=﹣2x+6,令x=t,得y=6﹣2t,
∴J(t,6﹣2t).
S=S△PBJ﹣S△PBK= ![]() PBPJ﹣
PBPJ﹣ ![]() PBPK=
PBPK= ![]() (3﹣t)(6﹣2t)﹣
(3﹣t)(6﹣2t)﹣ ![]() (3﹣t)2=
(3﹣t)2= ![]() t2﹣3t+
t2﹣3t+ ![]() .
.
综上所述,S与t的函数关系式为:
S=  .
.
【解析】(1)首先用待定系数法求出抛物线的解析式,然后进一步确定点B,C的坐标;(2)分别求出△CDB三边的长度,利用勾股定理的逆定理判定△CDB为直角三角形;(3)△COB沿x轴向右平移过程中,分两个阶段:
(I)当0<t≤ ![]() 时,如答图2所示,此时重叠部分为一个四边形;
时,如答图2所示,此时重叠部分为一个四边形;
(II)当 ![]() <t<3时,如答图3所示,此时重叠部分为一个三角形.
<t<3时,如答图3所示,此时重叠部分为一个三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O内接正三角形,将△ABC绕点O顺时针旋转30°得到△DEF,DE分别交AB,AC于点M,N,DF交AC于点Q,则有以下结论:①∠DQN=30°;②△DNQ≌△ANM;③△DNQ的周长等于AC的长;④NQ=QC.其中正确的结论是 ①②③ .(把所有正确的结论的序号都填上) 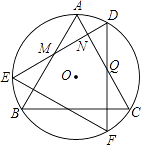
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表: 抽取的200名学生海选成绩分组表
组别 | 海选成绩x |
A组 | 50≤x<60 |
B组 | 60≤x<70 |
C组 | 70≤x<80 |
D组 | 80≤x<90 |
E组 | 90≤x<100 |
请根据所给信息,解答下列问题: 
(1)请把图1中的条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 , 表示C组扇形的圆心角θ的度数为度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师给爱好学习的小兵和小鹏提出这样一个问题:如图1,在△ABC中,AB=AC点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
小兵的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小鹏的证明思路是:如图2,过点P作PG⊥CF,垂足为G,先证△GPC≌△ECP,可得:PE=CG,而PD=GF,则PD+PE=CF.
请运用上述中所证明的结论和证明思路完成下列两题:
(1)如图3,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=16,CF=6,求PG+PH的值;
(2)如图4,P是边长为6的等边三角形ABC内任一点,且PD⊥AB,PF⊥AC,PE⊥BC,求PD+PE+PF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市举行的中学生安全知识竞赛中共有20道题.每一题答对得5分,答错或不答都扣3分.
(1)小李考了60分,那么小李答对了多少道题?
(2)小王获得二等奖(75~85分),请你算算小王答对了几道题?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=36°,∠C=72°,∠ABC的平分线交AC于D,则图中共有等腰三角形( )

A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com