
����Ŀ������ʦ������ѧϰ��С����С���������һ�����⣺��ͼ1������ABC�У�AB=AC��PΪ��BC�ϵ���һ�㣬����P��PD��AB��PE��AC������ֱ�ΪD��E������C��CF��AB������ΪF����֤��PD+PE=CF��
С����֤��˼·�ǣ���ͼ2������AP������ABP����ACP���֮�͵�����ABC���������֤�ã�PD+PE=CF��
С����֤��˼·�ǣ���ͼ2������P��PG��CF������ΪG����֤��GPC�ա�ECP���ɵã�PE=CG����PD=GF����PD+PE=CF��
��������������֤���Ľ��ۺ�֤��˼·����������⣺
��1����ͼ3����������ABCD��EF�۵���ʹ��D���ڵ�B�ϣ���C���ڵ�C�䴦����PΪ�ۺ�EF�ϵ���һ�㣬����P��PG��BE��PH��BC������ֱ�ΪG��H����AD=16��CF=6����PG+PH��ֵ��
��2����ͼ4��P�DZ߳�Ϊ6�ĵȱ�������ABC����һ�㣬��PD��AB��PF��AC��PE��BC����PD+PE+PF��ֵ��

���𰸡���1��C'B=AB=EQ=8����2��3![]() ��
��
��������
��1����������BEF������ֱ���![]() BF��PG+PH����
BF��PG+PH����![]() BFEQ��ʾ��Ȼ����������ת���߶�֮��Ĺ�ϵ���ɵó���.
BFEQ��ʾ��Ȼ����������ת���߶�֮��Ĺ�ϵ���ɵó���.
(2)���������ABC��������ٸ���������ABC�����=�����������ε�����ͽ���ת�����ɵó���.
�⣺��1����ͼ3������E��EQ��BC��Q������BP��
���ı���ABCD�dz����Σ�
��AD��BC��
���۵��ɵã���DEF=��BEF��
���BFE=��BEF��
��BE=BF��
��PG��BE��PH��BC��
��S��BEF=S��BEP+S��BFP=![]() BEPG+
BEPG+![]() BFPH=
BFPH=![]() BF��PG+PH����
BF��PG+PH����
��S��BEF=![]() BFEQ��
BFEQ��
��PG+PH=EQ��
���ı���ABCD�dz����Σ�
��AD=BC����C=��ADC=90�㣮
��AD=16��CF=6��
��BF=BC��CF=AD��CF=10��
DF=BF=10��CF=6,
�����ݹ��ɶ�����DC=8
S��BEF=![]() BFEQ=
BFEQ=![]() BF��DC=40
BF��DC=40
��![]() BF��PG+PH��=40
BF��PG+PH��=40
����PG+PH=8
��2����A��AM��BC������PA��PB��PC����ͼ4��ʾ��
�ߡ�ABCΪ�ȱ������εı߳�Ϊ6��AM��BC��
��MΪBC���е㣬��BM=CM=3��
��Rt��ABM��AB=6��BM=3��
���ݹ��ɶ����ã�AM=3![]()
����S��ABC=S��ABP+S��BPC+S��ACP
=![]() PEBC+
PEBC+![]() PFAC+
PFAC+![]() PDAB=
PDAB=![]() AB��PE+PF+PD��=
AB��PE+PF+PD��=![]() BCAM��
BCAM��
�ࣨPE+PF+PD��=AM=3![]() ��
��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=8��BC=12����E��BC���е㣬����AE������ABE��AE�۵�����B���ڵ�F��������FC����sin��ECF=�� �� 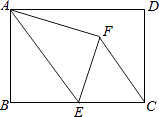
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��![]() ��˫����
��˫����![]() ����
����![]() ���㣬�ҵ�
���㣬�ҵ�![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��

��1����![]() ��ֵ��
��ֵ��
��2����˫����![]() ��һ��
��һ��![]() ��������Ϊ8����
��������Ϊ8����![]() �������
�������
��3����ԭ��![]() ����һ��ֱ��
����һ��ֱ��![]() ��˫����
��˫����![]() ��
��![]() ���㣨
���㣨![]() ���ڵ�һ���ޣ������ɵ�
���ڵ�һ���ޣ������ɵ�![]() Ϊ������ɵ��ı������Ϊ
Ϊ������ɵ��ı������Ϊ![]() �����
�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=����x��1��2+c��x�ύ��A��B��A��B�ֱ���y����������ࣩ���㣬��y��������ύ�ڵ�C������ΪD����֪A����1��0����
��1�����B��C�����ꣻ
��2���жϡ�CDB����״��˵�����ɣ�
��3������COB��x������ƽ��t����λ���ȣ�0��t��3���õ���QPE����QPE���CDB�ص����֣���ͼ����Ӱ���֣����ΪS����S��t�ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC��BC��AC=BC=4����ACΪֱ������Բ��Բ��Ϊ��O���Ե�CΪԲ�ģ�BCΪ�뾶�� ![]() ������O��BC��ƽ���߽������ڵ�D��E������Ӱ���ֵ������ ��
������O��BC��ƽ���߽������ڵ�D��E������Ӱ���ֵ������ �� 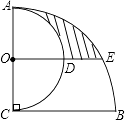
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����C����ABΪֱ���İ�Բ�ϣ���CAB��ƽ����AD��BC�ڵ�D����O����A��D���㣬��Բ��O��AB�ϣ�
��1����֤��BD�ǡ�O�����ߣ�
��2���� ![]() ��
�� ![]() �����O�������
�����O�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣��ڵ������������ȳ�������AB��CD������֮��������һ����������״�����ӣ�����ͼ�е�ֱ������ϵ���������ӿ�����y= ![]() x2��
x2�� ![]() x+3��ʾ
x+3��ʾ 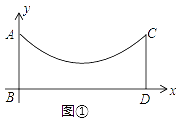
��1��������������͵������ľ��룻
��2��������ʵ����Ҫ��Ҫ����������֮���ټ�һ������EF�����ӽ���֧�ţ���ͼ�ڣ�����֪����EF��AB����Ϊ3m�����Ե�����Ҳ����������״��������EF������ӵ���͵㵽EF�ľ���Ϊ1m��������ľ���Ϊ1.8m��������EF�ij���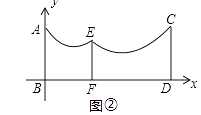
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ɽֲ��������A��B����������֪A��Ϊ�����Σ���Ϊ��x+y���ף���Ϊ��x��y���ף�B��Ϊ�����Σ��߳�Ϊ��x+3y���ף�
��1�����ô���ʽ��ʾA��B���������֮�Ͳ�����
��2���ָ���ʵ����Ҫ��A���������ģ������ӣ�11x��y���ף������٣�x��2y���ף����ĺ�A���ij��ȿ���350�ף������ĺ��������ܳ�֮��Ϊ980�ף�
����x��y��ֵ��
����A��ȫ����ֲC�ֻ���B��ȫ����ֲD�ֻ�����C��D���ֻ�Ͷ��ķ����������ο͵����������

�����ĺ�A��B�������εľ�����֮�ͣ���������=���橁Ͷ�룩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P�ǵȱ�������ABC�ڲ�һ�����㣬��APB=120�㣬��O�ǡ�APB�����Բ��AP��BP���ӳ��߷ֱ�BC��AC��D��E�� 
��1����֤��CA��CB�ǡ�O�����ߣ�
��2����֪AB=6��G��BC�ϣ�BG=2����PGȡ����Сֵʱ����PG�ij�����BGP�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com