
【题目】已知,点C在以AB为直径的半圆上,∠CAB的平分线AD交BC于点D,⊙O经过A、D两点,且圆心O在AB上.
(1)求证:BD是⊙O的切线.
(2)若 ![]() ,
, ![]() ,求⊙O的面积.
,求⊙O的面积.
【答案】
(1)解:连接OD.
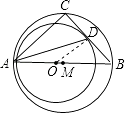
∵AB为直径,
∴∠ACB=90°,
∵OA=OD,
∴∠ODA=∠OAD,
∵AD平分∠CAB,
∴∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∴∠ODB=∠ACB=90°,
∴BD是⊙O的切线.
(2)解:∵ ![]() ,
,
∴AB=4AC,
∵BC2=AB2﹣AC2,
∴15AC2=80,
∴AC= ![]() ,
,
∴AB=4 ![]() .
.
设⊙O的半径为r,
∵OD∥AC,
∴△BOD∽△BAC,
∴ ![]()
∴  ,解得:r=
,解得:r= ![]()
∴πr2=π( ![]() )2=
)2= ![]() ,
,
∴⊙O的面积为 ![]() .
.
【解析】(1)连接OD,求出∠CAD=∠OAD=∠ADO,推出OD∥AC,推出OD⊥CB,根据切线判定推出即可;(2)根据勾股定理求出AC= ![]() ,AB=4
,AB=4 ![]() .设⊙O的半径为r,证△BOD∽△BAC,得出
.设⊙O的半径为r,证△BOD∽△BAC,得出 ![]() ,代入求出r即可.
,代入求出r即可.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对切线的判定定理的理解,了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】规定:求若干个相同的有理数的除法运算叫做除方,如2÷2÷2,(-3)÷(-3)÷(-3)÷(-3)等.类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方”,(-3)÷(-3)÷(-3)÷(-3)记作(-3)④,读作“-3的圈4次方”一般地,把![]() (a≠0)记作a,读作“a的圈c次方” .关于除方,下列说法正确的个数是( )
(a≠0)记作a,读作“a的圈c次方” .关于除方,下列说法正确的个数是( )
①任何非零数的圈2次方都等于1;②对于任何正整数c,1=1;③4③=3④ ;④负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表: 抽取的200名学生海选成绩分组表
组别 | 海选成绩x |
A组 | 50≤x<60 |
B组 | 60≤x<70 |
C组 | 70≤x<80 |
D组 | 80≤x<90 |
E组 | 90≤x<100 |
请根据所给信息,解答下列问题: 
(1)请把图1中的条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 , 表示C组扇形的圆心角θ的度数为度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师给爱好学习的小兵和小鹏提出这样一个问题:如图1,在△ABC中,AB=AC点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
小兵的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小鹏的证明思路是:如图2,过点P作PG⊥CF,垂足为G,先证△GPC≌△ECP,可得:PE=CG,而PD=GF,则PD+PE=CF.
请运用上述中所证明的结论和证明思路完成下列两题:
(1)如图3,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=16,CF=6,求PG+PH的值;
(2)如图4,P是边长为6的等边三角形ABC内任一点,且PD⊥AB,PF⊥AC,PE⊥BC,求PD+PE+PF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABDC中,∠D=∠B=90°,点O为BD的中点,且AO平分∠BAC.
(1)求证:CO平分∠ACD;
(2)求证:OA⊥OC;
(3)求证:AB+CD=AC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市举行的中学生安全知识竞赛中共有20道题.每一题答对得5分,答错或不答都扣3分.
(1)小李考了60分,那么小李答对了多少道题?
(2)小王获得二等奖(75~85分),请你算算小王答对了几道题?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动,如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:
(1)当t=3秒时,这时,P,Q两点之间的距离是多少?
(2)若△CPQ的面积为S,求S关于t的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
(1)如图1,已知△ABC,以AB,AC为边分别向△ABC外作等边△ABD和等边△ACE,连结BE,CD,请你完成图形(尺规作图,不写作法,保留作图痕迹),并证明:BE=CD;
(2)如图2,利用(1)中的方法解决如下问题:在四边形ABCD中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,求BD的长.
(3)如图3,四边形ABCD中,∠CAB=90°,∠ADC=∠ACB=α,tanα= ![]() ,CD=5,AD=12,求BD的长.
,CD=5,AD=12,求BD的长.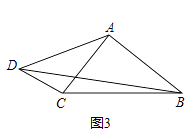
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com