
【题目】如图,A,C,B三点在同一条直线上,△DAC和△EBC都是等边三角形,AE,BD分别与CD,CE交于点M,N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN,其中正确结论的个数是( )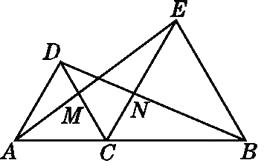
A.3
B.2
C.1
D.0
【答案】B
【解析】解:∵△DAC和△EBC都是等边三角形 ,
∴AC=CD,CE=BC,∠ACD=∠ECB=60° ,
∴∠ACE=∠DCB ,
∴△ACE≌△DCB(SAS) 。 ①符合题意;
∵ △ACE≌△DCB ,
∴∠AEC=∠DBC
∵∠DCE+∠ACD+∠ECB=180°,∠ACD=∠ECB=60°
∴∠DCE=∠ECB=60° ,
∵CE=BC,
∴△EMC≌△BNC(ASA)
∴CM=CN ,②符合题意 ;
∵AC=DC 在△DNC中,DC所对的角为∠DNC=∠NCB+∠NBC=60°+∠NBC>60°,而DN所对的角为60°,根据三角形中等边对等角、大边对大角,小边对小角的规律,则DC>DN,即是AC>DN,③不符合题意;
∴正确的结论有两个.
故应选:B 。
根据等边三角形的性质AC=CD,CE=BC,∠ACD=∠ECB=60° ,根据等式的性质得出∠ACE=∠DCB ,从而利用SAS判断出△ACE≌△DCB ;根据全等三角形对应角相等得出∠AEC=∠DBC ,根据平角的定义得出∠DCE=∠ECB=60° ,然后利用ASA判断出△EMC≌△BNC ,根据全等三角形对应边相等得出CM=CN ;AC=DC 在△DNC中,DC所对的角为∠DNC=∠NCB+∠NBC=60°+∠NBC>60°,而DN所对的角为60°,根据三角形中等边对等角、大边对大角,小边对小角的规律,则DC>DN,即是AC>DN;从而得出结论。


科目:初中数学 来源: 题型:
【题目】陆地上最高处是珠穆朗玛峰的峰顶,高出海平面约8844m,记为+8844m;陆地上最低处是死海,低于海平面约415m,记为______m,珠穆朗玛峰比死海高______m;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确结论的个数为( )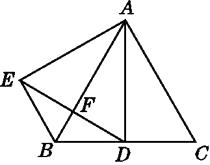
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.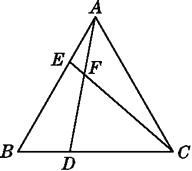
(1)求证:AD=CE;
(2)求∠DFC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲 乙两人在相同的条件下各射靶10次,射击成绩的平均数都是8环,甲射击成绩的方差是1.2,乙射击成绩的方差是1.8.下列说法中不一定正确的是( )
A.甲、乙射击成绩的众数相同
B.甲射击成绩比乙稳定
C.乙射击成绩的波动比甲较大
D.甲、乙射中的总环数相同
查看答案和解析>>
科目:初中数学 来源: 题型:
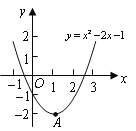
【题目】如图,已知二次函数![]() 的图象的顶点为A.二次函数
的图象的顶点为A.二次函数![]() 的图象与x轴交于原点O及另一点C,它的顶点B在函数
的图象与x轴交于原点O及另一点C,它的顶点B在函数![]() 的图象的对称轴上.
的图象的对称轴上.
(1)求点A与点C的坐标;
(2)当四边形AOBC为菱形时,求函数![]() 的关系式.
的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com