
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.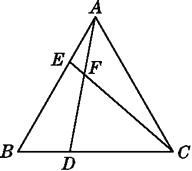
(1)求证:AD=CE;
(2)求∠DFC的度数.
【答案】
(1)证明:∵△ABC是等边三角形,
∴∠BAC=∠B=60°,AB=AC.
又∵AE=BD,
∴△AEC≌△BDA(SAS).
∴AD=CE 。
(2)解:∵ △AEC≌△BDA,
∴∠ACE=∠BAD.
∴∠DFC=∠FAC+∠ACE=∠FAC+∠BAD=∠BAC=60°
【解析】(1)根据等边三角形的性质得出∠BAC=∠B=60°,AB=AC ,然后利用SAS判断出△AEC≌△BDA ,根据全等三角形对应边相等得出AD=CE ;
(2)根据全等三角形对应角相等得出∠ACE=∠BAD,根据三角形的外角定理及等量代换得出∠DFC=∠FAC+∠ACE=∠FAC+∠BAD=∠BAC=60° 。


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象的对称轴是直线x=2,且图象过点(1,2),与一次函数y=x+m的图象交于(0,-1).
求两个函数解析式;
求两个函数图象的另一个交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线的对称轴是x=1,与x轴有两个交点,与y轴的交点坐标是(0,3),把它向下平移2个单位长度后,得到新的抛物线的解析式是y=ax2+bx+c,以下四个结论:
①b2﹣4ac<0,②abc<0,③4a+2b+c=1,④a﹣b+c>0中,其中正确的是_____(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
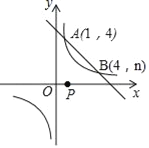
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,当PA+PB最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,C,B三点在同一条直线上,△DAC和△EBC都是等边三角形,AE,BD分别与CD,CE交于点M,N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN,其中正确结论的个数是( )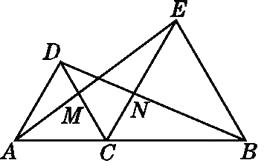
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学规定学生的学期体育成绩满分为100分,其中课外体育占20%,期中考试成绩占30%,期末考试成绩占50%.小彤的三项成绩(百分制)次为95,90,88,则小彤这学期的体育成绩为( )
A.89
B.90
C.92
D.93
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳环保,你我同行”.今年合肥市区的增设的“小黄车”、“摩拜单车”等公共自行车
给市民出行带来了极大的方便.图①是某种公共自行车的实物图,图②是该种公共自行车的
车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,
座杆CE=15cm,且∠EAB=75°.求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°
≈0.26,tan75°≈3.73)


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com