
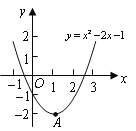
【题目】如图,已知二次函数![]() 的图象的顶点为A.二次函数
的图象的顶点为A.二次函数![]() 的图象与x轴交于原点O及另一点C,它的顶点B在函数
的图象与x轴交于原点O及另一点C,它的顶点B在函数![]() 的图象的对称轴上.
的图象的对称轴上.
(1)求点A与点C的坐标;
(2)当四边形AOBC为菱形时,求函数![]() 的关系式.
的关系式.
【答案】(1)C(2,0);(2)![]() .
.
【解析】试题分析:(1)二次函数y=ax2+bx的顶点在已知二次函数抛物线的对称轴上,可知两个函数对称轴相等,因此先根据已知函数求出对称轴.根据函数解析式得出顶点A的坐标与对称轴,故可得出二次函数y=ax2+bx关于x=1对称,且函数与x轴的交点分别是原点和C点,所以点C和点O关于直线l对称,故可得出点C的坐标;
(2)因为四边形AOBC是菱形,根据菱形性质,可以得出点O和点C关于直线AB对称,点B和点A关于直线OC对称,因此,可求出点B的坐标,根据二次函数y=ax2+bx的图象经过点B(1,2),C(2,0),将B,C代入解析式得出ab的值,进而得出其解析式.
试题解析:(1)∵y=x2-2x-1=(x-1)2-2,
∴顶点A的坐标为(1,-2).
∵二次函数y=ax2+bx的图象与x轴交于原点O及另一点C,它的顶点B在函数y=x2-2x-1的图象的对称轴上.
∴二次函数y=ax2+bx的对称轴为:直线x=1,
∴点C和点O关于直线x=1对称,
∴点C的坐标为(2,0).
(2)因为四边形AOBC是菱形,所以点B和点A关于直线OC对称,
因此,点B的坐标为(1,2).
因为二次函数y=ax2+bx的图象经过点B(1,2),C(2,0),
所以![]()
解得![]() ,
,
所以二次函数y=ax2+bx的关系式为y=-2x2+4x.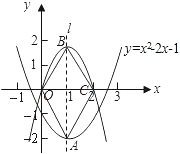


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,A,C,B三点在同一条直线上,△DAC和△EBC都是等边三角形,AE,BD分别与CD,CE交于点M,N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN,其中正确结论的个数是( )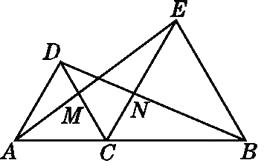
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一组数据x1 , x2 , …,xn的方差是s2 , 则新的一组数据ax1+1,ax2+1,…,axn+1(a为非零常数)的方差是(用含a和s2的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以扇形OAB的顶点O为原点,半径OB所在的直线为![]() 轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线
轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线![]() 与扇形OAB的边界总有两个公共点,则实数
与扇形OAB的边界总有两个公共点,则实数![]() 的取值范围是________________.
的取值范围是________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,线段A′B′是由线段AB经过平移得到的,已知点A(﹣2,1)的对应点为A′(3,﹣1),点B的对应点为B′(4,0),则点B的坐标为( )
A.(9,﹣1)
B.(﹣1,0)
C.(3,﹣1)
D.(﹣1,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com