如图，平面直角坐标系中，直线y=-x+a与x、y轴的正半轴分别交于点B和点A，与反比例函数y=-
的图象交于点C，若BA：AC=2：1，则a的值为（ ）
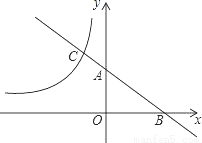
A．2 B．-2 C．3 D．-3
阅读快车系列答案科目：初中数学 来源：2015-2016学年江苏无锡南闸实验学校八年级下第一次月考数学试卷（解析版） 题型：选择题
如图，在△ABC中，AB=3，AC=4，BC=5，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为（ ）
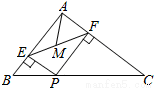
A．1 B．1.2 C．1.3 D．1.5
查看答案和解析>>
科目：初中数学 来源：2016届天津市河东区中考模拟数学试卷（解析版） 题型：填空题
如图，在平面直角坐标系中，将矩形AOCD沿直线AE折叠（点E在边DC上），折叠后端点D恰好落在边OC上的点F处．若点D的坐标为（10，8），则点E的坐标为 ．
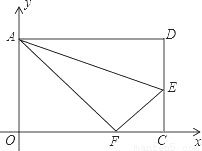
查看答案和解析>>
科目：初中数学 来源：2016届四川省自贡市六校中考二模数学试卷（解析版） 题型：解答题
倡导研究性学习方式，着力教材研究，习题研究，是学生跳出题海，提高学习能力和创新能力的有效途径．下面是一案例，请同学们认真阅读、研究，完成“类比猜想”及后面的问题．
习题解答
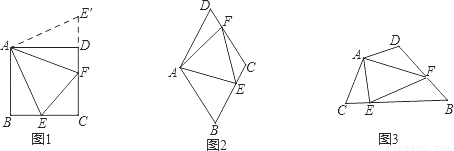
习题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，说明理由．
【解析】
∵正方形ABCD中，AB=AD，∠BAD=∠ADC=90°
∴把△ABE绕点A逆时针旋转90°至△ADE′，点F、D、E′在一条直线上．
∴∠E′AF=90°-45°=45°=∠EAF．
又∵AE′=AE，AF=AF
∴△AE′FF≌△AEF（SAS）
∴EF=E′F=DE′+DF=BE+DF．
习题研究．
观察分析：
观察图1，由解答可知，该题有用的条件是①．ABCD是四边形，点E、F分别在边BC、CD上；②．AB=AD；③．∠B=∠D=90°∠；④．∠EAF=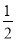
∠BAD．
类比猜想：
在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B=∠D时，还有EF=BE+DF吗？
要解决上述问题，可从特例入手，请同学们思考：如图2，在菱形ABCD中，点E、F分别在BC、CD上，当∠BAD=120°，∠EAF=60°时，还有EF=BE+DF吗？试证明．
（2）在四边形ABCD中，点E、F分别在边BC、CD上，当AB=AD，∠B+∠D=180°，∠EAF=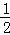
∠BAD时，还有EF=BE+DF吗？使用图3证明．
归纳概括：
反思前面的解答，思考每个条件的作用，可以得到一个结论“EF=BE+DF”的一般命题： ．
查看答案和解析>>
科目：初中数学 来源：2016届四川省自贡市六校中考二模数学试卷（解析版） 题型：选择题
据统计，今年春节期间（除夕到初五），微信红包总收发次数达321亿次，几乎覆盖了全国75%的网民，数据“321亿”用科学记数法可表示为（ ）
A．3.21×108 B．321×108
C．321×109 D．3.21×1010
查看答案和解析>>
科目：初中数学 来源：2016届山东省潍坊市中考一模数学试卷（解析版） 题型：解答题
如图，在△ABC中，∠ABC=∠ACB，以AC为直径的⊙O分别交AB、BC于点M、N，点P在AB的延长线上，且∠CAB=2∠BCP．
（1）求证：直线CP是⊙O的切线；
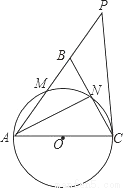
（2）若BC=2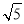
，sin∠BCP=
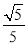，求点B到AC的距离．
查看答案和解析>>
科目：初中数学 来源：2016年初中毕业升学考试（山西卷）数学（解析版） 题型：填空题
如图是一组有规律的图案，它们是由边长相同的小正方形组成，其中部分小正方形涂有阴影，依此规律，第n个图案中有______________个涂有阴影的小正方形（用含有n的代数式表示）．
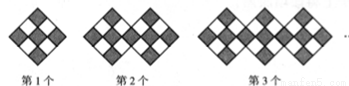
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，其中x=2+
．