
 如图,DB为半圆的直径,且 BD=2,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F.
如图,DB为半圆的直径,且 BD=2,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F.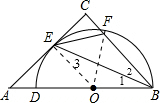


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、做抛掷硬币的实验,如果没有硬币用图钉代替硬币,做出的实验结果是一致的 |
| B、抛掷一枚质地均匀的硬币,已连续掷出5次正面,则第6次一定掷出背面 |
| C、某种彩票中奖的概率是1%,因此买100张该彩票一定会中奖 |
| D、天气预报说明天下雨的概率是50%,也就是说明天下雨和不下雨的机会是均等的 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,反比例函数y=
如图,反比例函数y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、通常加热到100℃时,水沸腾 |
| B、某射击运动员射击一次,命中靶心 |
| C、若a是实数,则|a|≥0 |
| D、在一个仅装着白球和黑球的袋中摸球,摸出红球 |
查看答案和解析>>
科目:初中数学 来源: 题型:
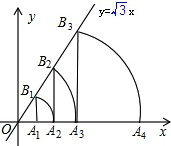 如图,直线y=
如图,直线y=| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com