
【题目】如图,△ABC 中,BD、CE分别是AC、AB上的高,BD与CE交于点O.BE=CD
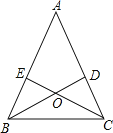
(1)问△ABC为等腰三角形吗?为什么?
(2)问点O在∠A的平分线上吗?为什么?
【答案】(1)△ABC是等腰三角形,理由见解析;(2)点O在∠A的平分线上,理由见解析.
【解析】
试题分析:(1)先利用HL证明Rt△BCD与Rt△CBE全等,然后根据全等三角形对应角相等可得∠ABC=∠ACB,再根据等角对等边的性质可得AB=AC,所以△ABC是等腰三角形;
(2)根据(1)中Rt△BCD≌Rt△CBE,然后利用全等三角形对应边相等可得BD=CE,对应角相等可得∠BCE=∠CBD,然后利用等角对等边可得BO=CO,相减可得OD=OE,再根据到角的两边距离相等的点在角的平分线上即可证明.
解:(1)△ABC是等腰三角形.
理由如下:∵BD、CE是△ABC的高,
∴△BCD与△CBE是直角三角形,
在Rt△BCD与Rt△CBE中,![]() ,
,
∴Rt△BCD≌Rt△CBE(HL),
∴∠ABC=∠ACB,
∴AB=AC,
即△ABC是等腰三角形;
(2)点O在∠A的平分线上.
理由如下:∵Rt△BCD≌Rt△CBE,
∴BD=CE,∠BCE=∠CBD,
∴BO=CO,
∴BD﹣BO=CE﹣CO,
即OD=OE,
∵BD、CE是△ABC的高,
∴点O在∠A的平分线上(到角的两边距离相等的点在角的平分线上).


科目:初中数学 来源: 题型:
【题目】两条平行线被第三条直线所截,则下列说法错误的是( )
A. 一对邻补角的平分线互相垂直 B. 一对同位角的平分线互相平行
C. 一对内错角的平分线互相平行 D. 一对同旁内角的平分线互相平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为( )
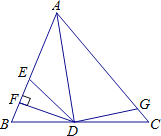
A.11 B.5.5 C.7 D.3.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在直角坐标平面内,抛物线y=x2+bx+c经过点A(2,0)、B(0,6).
(1)求抛物线的表达式;
(2)抛物线向下平移几个单位后经过点(4,0)?请通过计算说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com