
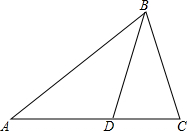
 如图,△ABC中,BD是△ABC的角平分线,
如图,△ABC中,BD是△ABC的角平分线,分析 (1)利用基本作图(作已知线段的垂直平分线)作MN垂直平分BD;
(2)先根据线段垂直平分线的性质得MB=MD,NB=ND,再利用BD平分∠MBN,BD⊥MN可判断△BMN为等腰三角形,则BM=BN,所以BM=MD=DN=NB,于是可判断四边形BMDN为菱形.
解答 解:(1)如图,MN为所作;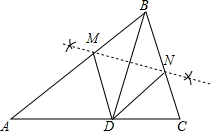
(2)四边形BMDN为菱形.理由如下:
∵MN垂直平分BD,
∴MB=MD,NB=ND,
∵BD平分∠MBN,BD⊥MN,
∴△BMN为等腰三角形,
∴BM=BN,
∴BM=MD=DN=NB,
∴四边形BMDN为菱形.
点评 本题考查了基本作图:作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线.也考查了菱形的判定.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(3,0),B(0,$\sqrt{3}$)两点,点C为线段AB上的一动点,过点C作CD⊥x轴于点D.
如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(3,0),B(0,$\sqrt{3}$)两点,点C为线段AB上的一动点,过点C作CD⊥x轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m≠n | B. | m≠-n | C. | np≠-mq | D. | p≠-q,m≠n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com